Bonsoir à tous.
Je suis tombée sur une série d'exos et je galère à résoudre quelques uns de ses exercices. Merci de bien vouloir me donner un coup de main.
Voici les énoncés :
Ensembles :
Soient A et B deux parties d'un ensemble E :
On considère dans P(E) l'équation : X U (A\B) = A
1) Mq si X est solution de l'équation alors AnB C X C A
2) Déduire l'ensemble de solutions de l'éq.
3) Déduire les solutions de l'éq. dans le cas : A={1,2,4} et B={1,3}
Récurrence :
On pose pour tout n € N*:
Tn = 1-2+3-4+....+((-1)^(n+1))n
1)a)Mq ( pour tt n € N*) T2n = -n
b) ( pour tt n € N*) T2n+1 = (n+1)
2) Mq (pour tt n € N*) (2^(n-1))(n+2) =< 3^n
Merci d'avance.
Bonne fin de soirée !
Ensembles et logique
5 messages
- Page 1 sur 1
Re: Ensembles et logique
Salut !
Exo 1. Qu'as-tu essayé de faire pour l'instant ? Où bloques-tu ?
As-tu pensé à faire des diagrammes de Venn (des dessins de patates quoi) ?
1. L'inclus est facile, je te laisse y réfléchir si besoin.
est facile, je te laisse y réfléchir si besoin.
Pour montrer que , montre que
, montre que  . Déduis-en alors l'inclusion voulue.
. Déduis-en alors l'inclusion voulue.
De toute façon, il faut nécessairement se servir de l'équation = A) .
.
Pour rappel : , où
, où 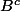 désigne le complémentaire de
désigne le complémentaire de  dans
dans  .
.
2. Montre qu'on a la réciproque de la question précédente : si est une partie de
est une partie de  vérifiant
vérifiant  alors
alors =A) .
.
Résoudre dans) l'équation d'inconnue
l'équation d'inconnue  :
: =A) revient finalement à résoudre la double inclusion
revient finalement à résoudre la double inclusion  .
.
Exo 2. tout est dit dans le titre de l'exercice : utilise le raisonnement par récurrence.
Sinon, il y a une méthode plus directe qui consiste à faire du "télescopage" pour les questions 1. et 2.
1. Montre que pour tout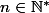 ,
, } - T_{2n} = {-1}) . En remarquant que
. En remarquant que } - T_{2k} )) , déduis-en le résultat voulu.
, déduis-en le résultat voulu.
2. Même idée en considérant+1} - T_{2n+1}) .
.
Exo 1. Qu'as-tu essayé de faire pour l'instant ? Où bloques-tu ?
As-tu pensé à faire des diagrammes de Venn (des dessins de patates quoi) ?
1. L'inclus
Pour montrer que
De toute façon, il faut nécessairement se servir de l'équation
Pour rappel :
2. Montre qu'on a la réciproque de la question précédente : si
Résoudre dans
Exo 2. tout est dit dans le titre de l'exercice : utilise le raisonnement par récurrence.
Sinon, il y a une méthode plus directe qui consiste à faire du "télescopage" pour les questions 1. et 2.
1. Montre que pour tout
2. Même idée en considérant
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Ensembles et logique
Excusez-moi, mais je ne vous suis pas. Je n'arrive pas à réellement capter vos propositions..je n'ai nulle idée sur la manière dont il faut procéder. Pourriez-vous être plus précis, svp?
Re: Ensembles et logique
Bonjour pour t'aider un peu , je vais expliciter un peu plus le début de la solution donnée par @CNuggets:
Hypothèse: X U (A\B) = A
Conclusion:
raisonnement: soit x un élément quelconque de X. Alors x appartient X U (A\B) donc à A. On a montré que tout élément de X est dans A, autrement dit
Si tu montres (comme le suggère @Nuggets) alors on aura bien
(comme le suggère @Nuggets) alors on aura bien  puisque évidement on a
puisque évidement on a 
Montrons alors que
D'abord une inclusion dans un sens est évidente: En effet, on sait que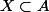 donc
donc 
Vérifions l'inclusion dans l'autre sens. Soit x un élément quelconque de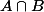 . Bien entendu x appartient à A et à B et il faut montrer que x appartient à X. Mais d'après l'hypothèse A=X U (A\B), x appartient à X ou (non exclusif) à (A\B). Mais x n'est pas dans (A\B) car x appartient à B. Donc x appartient à X.....
. Bien entendu x appartient à A et à B et il faut montrer que x appartient à X. Mais d'après l'hypothèse A=X U (A\B), x appartient à X ou (non exclusif) à (A\B). Mais x n'est pas dans (A\B) car x appartient à B. Donc x appartient à X.....
Voilà tu peux continuer ainsi les indications de @Nugetts comme je viens de le faire... Mais pour avoir plus de recul, il est conseillé de faire des dessins ça aide bien....
Hypothèse: X U (A\B) = A
Conclusion:
1. L'inclusest facile, je te laisse y réfléchir si besoin.
raisonnement: soit x un élément quelconque de X. Alors x appartient X U (A\B) donc à A. On a montré que tout élément de X est dans A, autrement dit
Pour montrer que, montre que
Déduis-en alors l'inclusion voulue......
De toute façon, il faut nécessairement se servir de l'équation. Pour rappel .....
Si tu montres
Montrons alors que
D'abord une inclusion dans un sens est évidente: En effet, on sait que
Vérifions l'inclusion dans l'autre sens. Soit x un élément quelconque de
Voilà tu peux continuer ainsi les indications de @Nugetts comme je viens de le faire... Mais pour avoir plus de recul, il est conseillé de faire des dessins ça aide bien....
Re: Ensembles et logique
Merci beaucoup! J'arrive à beaucoup mieux comprendre.
Qu'en est-il des solutions?
Qu'en est-il des solutions?
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
