Bonjour.
Je suis en 1°S et j'ai un gros problème par rapport aux ensembles de définition des fonctions, surtout lorsqu'on parle de fonctions composées.
Je ne comprends rien (non, le mot n'est, malheureusement, pas exagéré.)
Est ce que quelqu'un aurait la gentillesse de tout m'expliquer ? :hein2:
Merci beaucoup !
Ensemble de définition des fonctions.
6 messages
- Page 1 sur 1
Salut,
voici un super doc, j'espère que ça t'aidera.
http://pagesperso-orange.fr/gilles.costantini/Lycee_fichiers/CoursP_fichiers/compfct.pdf
Si tu as encore des questions nous sommes là
voici un super doc, j'espère que ça t'aidera.
http://pagesperso-orange.fr/gilles.costantini/Lycee_fichiers/CoursP_fichiers/compfct.pdf
Si tu as encore des questions nous sommes là
partir de la fin (dernière fonction composée)
bonjour,
ce n'est pas simple.
par exemple, avec trois fonctions f,g,h
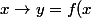 \rightarrow z=g(y)=g(f(x)) \rightarrow u=h(z)=h(g(f(x))))
il faut et il suffit que(x) \in D_h) et
et  \in D_g) et
et 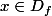
où
D_f est le domaine de définition de f,
D_g est le domaine de définition de g,
D_h est le domaine de définition de h.
exemple:
Si l'on compose les trois fonctions.
on essaye de déterminer le domaine de définition de la composée
sans calculer la composée
^2 \\<br />h: z \rightarrow \sqrt{z-4})
si on compose f puis g puis h
on obtient u=h(z)=h(g(y))=(h(g(f(x)))
il faut et il suffit que
(la dernière fonction composée)
mais z, c'est^2) ,ie, une image par g
,ie, une image par g
d'où
^2 - 4 \geq 0)
on factorise
(y+1) \geq 0)
donc y appartient à la réunion des intervalles

mais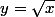 . c'est une image par f !
. c'est une image par f !
la condition
 n'est jamais réalisée.
n'est jamais réalisée.
Comme c'est une réunion de deux intervalles, on réalise l'autre condition

comme y est une racine carrée
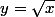
c'est donc que
ce n'est pas simple.
par exemple, avec trois fonctions f,g,h
il faut et il suffit que
où
D_f est le domaine de définition de f,
D_g est le domaine de définition de g,
D_h est le domaine de définition de h.
exemple:
Si l'on compose les trois fonctions.
on essaye de déterminer le domaine de définition de la composée
sans calculer la composée
si on compose f puis g puis h
on obtient u=h(z)=h(g(y))=(h(g(f(x)))
il faut et il suffit que
(la dernière fonction composée)
mais z, c'est
d'où
on factorise
donc y appartient à la réunion des intervalles
mais
la condition
Comme c'est une réunion de deux intervalles, on réalise l'autre condition
comme y est une racine carrée
c'est donc que
autre exemple, avec trois homographies

on compose par f puis g puis h
on regarde la dernière composée h.
on a des souçis si z=2
mais
donc des souçis dans deux cas:
 ou y=3
ou y=3
on résoud la 1ère équation
y-2=2y-6
y=4 ou y=3
mais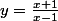
on résoud donc les équations
x+1=4(x-1) ou x+1=3(x-1)
soit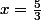 ou
ou 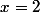
les valeurs interdites pour hogof sont donc

on compose par f puis g puis h
on regarde la dernière composée h.
on a des souçis si z=2
mais
donc des souçis dans deux cas:
on résoud la 1ère équation
y-2=2y-6
y=4 ou y=3
mais
on résoud donc les équations
x+1=4(x-1) ou x+1=3(x-1)
soit
les valeurs interdites pour hogof sont donc
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
