Difficile équation !
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Jaafar Aitraf
- Membre Naturel
- Messages: 48
- Enregistré le: 25 Déc 2012, 19:44
-
 par Jaafar Aitraf » 26 Déc 2012, 14:25
par Jaafar Aitraf » 26 Déc 2012, 14:25
Bonjour les matheux ! Ca vaa !
Voilà, pour aujourd'hui j'ai une bonne équation pour se casser la tête avec !
* Sachant que : 2(a²/b²+b²/a²)-3(a/b+b/a)-1=0
Trouve a/b !
:hum:

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 26 Déc 2012, 14:38
par Ericovitchi » 26 Déc 2012, 14:38
Bonjour, Le plus simple est de poser x=a/b et de regarder quelle équation en x ça donne.
Ou encore mieux poser z=x+1/x donc a/b+b/a
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Déc 2012, 14:38
par Kikoo <3 Bieber » 26 Déc 2012, 14:38
Jaafar Aitraf a écrit:Bonjour les matheux ! Ca vaa !
Voilà, pour aujourd'hui j'ai une bonne équation pour se casser la tête avec !
* Sachant que : 2(a²/b²+b²/a²)-3(a/b+b/a)-1=0
Trouve a/b !
:hum:
Hello,
On remplace a/b par un réel x.
L'équation devient 2x² - 3x + 2/x² - 3/x = 1
Equation de deg 4 : 2x^4 - 3x^3 + x² - 3x + 2 = 0
Et je te laisse voir si tu peux faire quelque chose de cette équation !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Déc 2012, 14:42
par Kikoo <3 Bieber » 26 Déc 2012, 14:42
Ericovitchi a écrit:Bonjour, Le plus simple est de poser x=a/b et de regarder quelle équation en x ça donne.
Ou encore mieux poser z=x+1/x donc a/b+b/a
Le deuxième est sans doute le meilleur, je me rappelle d'une résolution d'équation de degré 4 avec ce changement de variable !
-
Jaafar Aitraf
- Membre Naturel
- Messages: 48
- Enregistré le: 25 Déc 2012, 19:44
-
 par Jaafar Aitraf » 26 Déc 2012, 14:42
par Jaafar Aitraf » 26 Déc 2012, 14:42
Bon je pense que la meilleure solution est de poser x=a/b, je vais voir!
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Déc 2012, 14:44
par Kikoo <3 Bieber » 26 Déc 2012, 14:44
Jaafar Aitraf a écrit:Bon je pense que la meilleure solution est de poser x=a/b, je vais voir!
Je pense que c'est plutôt le deuxième

Laisse moi le temps de prendre un crayon et une feuille de papier :p
-
Jaafar Aitraf
- Membre Naturel
- Messages: 48
- Enregistré le: 25 Déc 2012, 19:44
-
 par Jaafar Aitraf » 26 Déc 2012, 14:50
par Jaafar Aitraf » 26 Déc 2012, 14:50
Kikoo <3 Bieber a écrit:Je pense que c'est plutôt le deuxième

Laisse moi le temps de prendre un crayon et une feuille de papier :p
xD Oké go !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Déc 2012, 15:00
par Kikoo <3 Bieber » 26 Déc 2012, 15:00
Tu devrais trouver 2 solutions réelles si je ne me suis pas trompé ;)
-
Jaafar Aitraf
- Membre Naturel
- Messages: 48
- Enregistré le: 25 Déc 2012, 19:44
-
 par Jaafar Aitraf » 26 Déc 2012, 15:06
par Jaafar Aitraf » 26 Déc 2012, 15:06
Je me bloque trop ! :'( !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Déc 2012, 15:08
par Kikoo <3 Bieber » 26 Déc 2012, 15:08
Vas y, pose z=a/b + b/a
que devient l'équation ?
-
Jaafar Aitraf
- Membre Naturel
- Messages: 48
- Enregistré le: 25 Déc 2012, 19:44
-
 par Jaafar Aitraf » 26 Déc 2012, 15:14
par Jaafar Aitraf » 26 Déc 2012, 15:14
On ne peut pas car on a a²/b² donc ce Z doit présenter juste une expression !

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 26 Déc 2012, 15:19
par Ericovitchi » 26 Déc 2012, 15:19
il faut utiliser (x+1/x)²=x²+1/x²+2 et donc remplacer x²+1/x² par (x+1/x)²-2
donc en fait a²/b²+b²/a² par z²-2

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 26 Déc 2012, 16:41
par chan79 » 26 Déc 2012, 16:41
Jaafar Aitraf a écrit:On ne peut pas car on a a²/b² donc ce Z doit présenter juste une expression !
comme cela a été dit, on peut poser z=a/b+b/a
on montre alors que si un couple (a,b) convient, alors deux valeurs seulement sont possibles pour z
Ensuite, dans chaque cas, on pose x=a/b
exemple de solution:
(a,b)=(2,1)
-
Jaafar Aitraf
- Membre Naturel
- Messages: 48
- Enregistré le: 25 Déc 2012, 19:44
-
 par Jaafar Aitraf » 26 Déc 2012, 17:57
par Jaafar Aitraf » 26 Déc 2012, 17:57
Ericovitchi a écrit:il faut utiliser (x+1/x)²=x²+1/x²+2 et donc remplacer x²+1/x² par (x+1/x)²-2
donc en fait a²/b²+b²/a² par z²-2
Sayez j'ai trouvé la soultion mais j'ai pas compris le truc que t'as dis :p ?!
" il faut utiliser (x+1/x)²=x²+1/x²+2 et donc remplacer x²+1/x² par (x+1/x)²-2 " comment faire!ù
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Déc 2012, 18:04
par Kikoo <3 Bieber » 26 Déc 2012, 18:04
tu remarques que
\not= 2\(\frac{a}{b}+\frac{b}{a}\)^2)
En effet,
^2=\frac{a^2}{b^2}+2+ \frac{b^2}{a^2})
d'où la nécessité de retrancher le 2, afin de ne se retrouver qu'avec
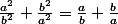^2-2)
PS : et qu'as-tu trouvé ?

-
Jaafar Aitraf
- Membre Naturel
- Messages: 48
- Enregistré le: 25 Déc 2012, 19:44
-
 par Jaafar Aitraf » 26 Déc 2012, 18:08
par Jaafar Aitraf » 26 Déc 2012, 18:08
J'ai trouver une équation degre 2 !
2(z²-2)-3z-1=0
2z²-3z-5 = 0
Alors deux solutions :
z = 5/2 ou z = -1 !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Déc 2012, 18:11
par Kikoo <3 Bieber » 26 Déc 2012, 18:11
Jaafar Aitraf a écrit:J'ai trouver une équation degre 2 !
2(z²-2)-3z-1=0
2z²-3z-5 = 0
Alors deux solutions :
z = 5/2 ou z = -1 !
C'est bien

Il te reste à trouver x=a/b !
-
Jaafar Aitraf
- Membre Naturel
- Messages: 48
- Enregistré le: 25 Déc 2012, 19:44
-
 par Jaafar Aitraf » 26 Déc 2012, 18:15
par Jaafar Aitraf » 26 Déc 2012, 18:15
C'est dur de trouver ce x ^_^
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Déc 2012, 18:17
par Kikoo <3 Bieber » 26 Déc 2012, 18:17
Pas tant que ça ! ;)
Souviens-toi que tu avais posé z = x + 1/x = a/b + b/a !
Il te reste donc deux équations à résoudre, mais lesquelles ?
-
Jaafar Aitraf
- Membre Naturel
- Messages: 48
- Enregistré le: 25 Déc 2012, 19:44
-
 par Jaafar Aitraf » 26 Déc 2012, 18:20
par Jaafar Aitraf » 26 Déc 2012, 18:20
Il faut trouver a/b et on a deux équations !
z = a/b+b/a
z²-2=a²/b²+b²/a²
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
