Devoir maison probabilité

[Samantha151709]

Le quart de la population est vaccinée contre cette maladie contagieuse. De plus on estime que sur la population vaccinée 90% des individus ne tombent pas malade. Sur la population totale, on estime aussi que 10% des individus sont malades.
On choisit au hasard un individu dans cette population. Sachant qu’un individu n’est pas vaccinée qu’elle est la probabilité qu’il tombe malade ?
Svp aidez moi je dois le rendre demain

[Sylviel]

Il faut commencer par faire un arbre avec les proba dont on dispose, ça aide à se représenter les choses.
Ensuite il faut introduire des notations :
pour l'évènement "l'individu est vacciné"
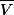pour l'évènement "l'individu n'est pas vacciné"
pour l'évènement "l'individu est malade"
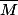pour l'évènement "l'individu n'est pas malade"

Je te laisse compléter (à partir du texte) :





Ensuite je te conseille de calculer la probabilité qu'il soit vacciné et non malade

Tu pourras en déduire (en le justifiant) la probabilité qu'il soit vacciné et malade, puis la probabilité qu'il soit non vacciné et malade. On obtiendra finalement la probabilité qu'il soit malade sachant qu'il est non vacciné.

[Samantha151709]

Il faut commencer par faire un arbre avec les proba dont on dispose, ça aide à se représenter les choses.
Ensuite il faut introduire des notations :
pour l'évènement "l'individu est vacciné"
pour l'évènement "l'individu n'est pas vacciné"
pour l'évènement "l'individu est malade"
pour l'évènement "l'individu n'est pas malade"

Je te laisse compléter (à partir du texte) :





Ensuite je te conseille de calculer la probabilité qu'il soit vacciné et non malade

Tu pourras en déduire (en le justifiant) la probabilité qu'il soit vacciné et malade, puis la probabilité qu'il soit non vacciné et malade. On obtiendra finalement la probabilité qu'il soit malade sachant qu'il est non vacciné.

D’accord tous d’abord merci mais comment trouve ton p(V)

[Sylviel]

"Sur la population totale, on estime aussi que 10% des individus sont malades."
"Le quart de la population est vaccinée contre cette maladie contagieuse. "

[Sylviel]

Pas d'aide par MP svp.

Que signifie, avec des mots, "P(V)" ?

[titine]

Comme le dit Sylviel il faut commencer par traduire l'énoncé en terme de probabilité :

Le quart de la population est vaccinée contre cette maladie contagieuse.

Donc si on prend une personne au hasard dans cette population, on a 1 chance sur 4 qu'elle soit vaccinée.
D'accord ?
Donc P(V) = ......

De plus on estime que sur la population vaccinée 90% des individus ne tombent pas malade.

Donc la probabilité qu'une personne prise au hasard soit malade sachant qu'elle est vaccinée est ....

Sur la population totale, on estime aussi que 10% des individus sont malades.

Donc P(M) = ....

[Samantha151709]

Pas d'aide par MP svp.

Que signifie, avec des mots, "P(V)" ?

Oui pardon et bien que c’est la probabilité qu’il soit vaccinée

[Samantha151709]

Comme le dit Sylviel il faut commencer par traduire l'énoncé en terme de probabilité :

Le quart de la population est vaccinée contre cette maladie contagieuse.

Donc si on prend une personne au hasard dans cette population, on a 1 chance sur 4 qu'elle soit vaccinée.
D'accord ?
Donc P(V) = ......

De plus on estime que sur la population vaccinée 90% des individus ne tombent pas malade.

Donc la probabilité qu'une personne prise au hasard soit malade sachant qu'elle est vaccinée est ....

Sur la population totale, on estime aussi que 10% des individus sont malades.

Donc P(M) = ....

Donc p(V) si j’ai bien compris est =0,25

[Sylviel]

Tu as 100 personnes. 25 sont vaccinées. Tu en prends une au hasard (uniformément). La probabilité qu'elle soit vaccinnée est donc "nombre de cas favorable"/"nombre de cas total" = 25/100 = 0.25

Oui, maintenant il faut compléter le reste.

[Samantha151709]

Tu as 100 personnes. 25 sont vaccinées. Tu en prends une au hasard (uniformément). La probabilité qu'elle soit vaccinnée est donc "nombre de cas favorable"/"nombre de cas total" = 25/100 = 0.25

Oui, maintenant il faut compléter le reste.

D’accord super merci beaucoup