Déterminer a et b

[lez321]

Bonjour à tous, j'ai besoin d'aide sur une petite question.
Je dois déterminer deux nombres a et b tels que, pour tout réel X, X^3 - 36X - 91 = (X - α) (X^2 + aX + b)
Sachant que α = 7

Merci d'avance pour votre aide !

[chan79]

salut
Développe le membre de droite et identifie les coefficients
ou bien regarde les coef de X² de chaque côté

[lez321]

Ah oui pas bête ! Alors quand je développe ça me donne :
(X-7) = (X^2 + aX + b)
(X-7) = X^3 + aX^2 + bX - 7X^2 - 7aX - 7b
(X-7) = X^3 + X^2 (7-a) + X (b-7a) - 7b

Sauf qu'après je bloque pour trouver a et b

[chan79]

en fait tu peux identifier avec:
X^3 - 36X - 91 =X^3 + X² (7-a) + X (b-7a) - 7b

[zygomatique]

Ah oui pas bête ! Alors quand je développe ça me donne :
(X-7) = (X^2 + aX + b)
(X-7) = X^3 + aX^2 + bX - 7X^2 - 7aX - 7b
(X-7) = X^3 + X^2 (7-a) + X (b-7a) - 7b

Sauf qu'après je bloque pour trouver a et b

n'a pas de sens ...

[lez321]

zygomatique, je me suis juste trompé : au lieu du égal je dois juste mettre le signe multiplié. Mais à part ça je pense que c'est juste

[WillyCagnes]

Ah oui pas bête ! Alors quand je développe ça me donne :
(X-7) = (X^2 + aX + b)
(X-7) = X^3 + aX^2 + bX - 7X^2 - 7aX - 7b
(X-7) = X^3 + X^2 (7-a) + X (b-7a) - 7b

Sauf qu'après je bloque pour trouver a et b

plutôt bêta...
(X-7) = (X^2 + aX + b) NON mais
(X-7) (X^2 + aX + b)
=x^3+x²(-7+a)+ x(b -7a) -7b à verifier

tu developperas cette expression et tu identifieras chacun des termes
X^3 - 36X - 91 = x^3+ x²(-7+a ) + x(b -7a) -7b
1=1
0=(-7+a)
-36 = (b-7a)
-91 = -7b
et tu resous le syteme

[lez321]

Pour trouver a je prends a-7=0
Donc on a
a-7=0
a=7

Et pour trouver c je prends b-7a=-36 mais du coup j'arrive pas à résoudre cette équation, comment je pourrais faire pour trouver b ?

[pascal16]

j'ai pas vérifié les autres calculs :
b-7a=-36
mais a=7
b-49=-36
b=-36+49
...

[lez321]

super j'ai compris merci beaucoup !

Cependant, j'ai une dernière petite question, pas vraiment en rapport avec les calcules précèdents :
on me demande de résoudre X^2 + 4X + 1= 0 (on est dans le monde des imaginaires si ça peut vous aider)

j'ai déjà essayé de calculer le discriminant mais ça ne marche pas

[chan79]

super j'ai compris merci beaucoup !

Cependant, j'ai une dernière petite question, pas vraiment en rapport avec les calcules précèdents :
on me demande de résoudre X^2 + 4X + 1= 0 (on est dans le monde des imaginaires si ça peut vous aider)

j'ai déjà essayé de calculer le discriminant mais ça ne marche pas

salut
Mets tes calculs et on verra où ça coince.

[lez321]

X^2 + 4X + 1 = 0

Δ = 4^2 - 4*1*1 = 12 > 0 donc deux solutions

x1 = (-4 + √12) / 2 ≈ -0,3
x2 = (-4 - √12) / 2 ≈ -3,7

Je me demande si c'est bon si les résultats sont négatifs?

[danyL]

X^2 + 4X + 1 = 0

Δ = 4^2 - 4*4*1 = 12 > 0 donc deux solutions --> il y a un 4 de trop

x1 = (-4 + √12) / 12 ≈ -0,3 --> pourquoi diviser par 12 ?
x2 = (-4 - √12) /12 ≈ -3,7

Je me demande si c'est bon si les résultats sont négatifs?

bonjour
des racines peuvent être négatives
pour vérifier si les résultats sont bons, tu peux remplacer x par x1 dans l'expression et la calculer : elle doit être égale à 0
est ce que (-0.3)² + 4 (-0.3) + 1 vaut 0 ?
de même pour x2

[lez321]

À la place du 4 c'est censé être un 1 et pour la division par 12 c'est censé être un 2, désolé je ne me suis pas relu (mais c'est bon je viens de modifier)

Si je remplace x par x1 ça me donne -0,11 et pareil pour x2. Que dois-je en déduire?

[zygomatique]

[danyL]

Si je remplace x par x1 ça me donne -0,11 et pareil pour x2. Que dois-je en déduire?

tu ne trouves pas tout à fait 0 parce que tu as gardé 1 seule décimale
en prenant x1 = -0.268 au lieu de -0.3 et x2 = -3.732 au lieu de -3.7 on obtient -0.000176

mais il vaut mieux garder la racine carrée, cela évite les approximations, et développer
on peut déjà simplifier √12
√12 = √ (4*3) = 2 √3

x1 = (-4 + √12) / 2 = (-4 + 2√3) / 2 = -2 + √3
x2 = (-4 - √12) / 2 = (-4 - 2√3) / 2 = -2 - √3

pour vérifier x2 :
( -2 - √3) (-2 - √3 ) + 4 ( -2 - √3) + 1
= (4 + 3 + 2*2√3) + ( -8 -4√3) + 1
= (7 + 4√3) -7 -4√3
= 0

[zygomatique]

il est effectivement temps de savoir que

en faisant attention que ce que j'ai écrit est mal écrit puisque la relation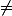 n'est pas transitive ...

[lez321]

MERCI BEAUCOUP à vous tous !

(malheureusement je n'avais pas vu les message et j'ai dû rendre ma copie sans y apporter de modifications, mais bon c'est pas grave ce n'était que pour une question)

merci encore pour votre aide