Determination de reels maissans chiffre

[Roneila]

VOilà:

J'ai un exercice pour les limites et on me dit:

soient a,b et c des réels avec c=/= 0. Soit f la fonction definie sur R\{-d/c}par : f(x)=(ax+b)/cx+d

determiner des réels ;), ;) et k tels que f(x)=;)+(k/(x-;))

Mais des réels sont des nombres, noms? alors comment faire sans un seul chiffre ?
je suis perdu et personne dans mon entourage n'a réussis à m'aider.

[laya]

Bonjour,
Remarque: corrigé ton énonce, tu dois dire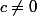
Comme beaucoup de lycéens, tu as encore un problème avec le calcul littéral.
Lorsqu'un énoncé te dit : soit a un nombre réel, il faut comprendre que "a" est un paramètre qui peut être égal à 5, à 1000 ou à 100000 ou à tout autre nombre réel. Ce dont on est sûr c'est qu'on l'a appelé "a".
Par exemple : le prix d'une minute de communication avec le portable est de 0.5€. Soit b un nombre entier positif. Quel est le prix d'un nombre "b" de minutes de communication ? Si on te suit, on répondrait, ben je ne peux pas dire combien ça va coûter puisque je ne connais pas le nombre de minutes "b". Or ce n'est pas ce qu'on attend comme réponse. On attend à ce que tu dises : le prix de "b" minutes de communication est de (0.5*b). C'est la seule réponse possible. Cela veut dire que si j'appelle pendant 2 minutes, b est égal à 2 et le prix est de 0.5*2. Si j'appelle pendant 5 minutes, b est égal à 5 et le prix est de 0.5*5, mais bon, on ne va pas s'amuser à faire tous les nombres entiers quand-même (impossible :lol3: ).

Revenons à ton exercice, on te demande en fait de trouver , k et en fonction des nombres que tu connais, c'est-à-dire : a, b, c et d.
Autrement dit, tu as une fonction sous une certaine forme et tu dois la réécrire autrement, juste lui donner un autre visage qui sera peut-être utile dans les questions suivantes.

Un exemple, Soit la fonction f définie sur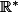 par :
, on peut la réécrire de cette façon, pour tout x dans son ensemble de définition :


Avant de continuer ton exo, dis-moi ce que valent, dans l'exemple ci-dessus, a, b, c, d puis

[Roneila]

Merci pour ton explication. C'est effectivement un point que je n'avais pas compris.
pour l'exercice,je ne suis vraiment pas sur de ce que je vais répondre:

a=2
b=1
c=1
d=0
et
;)=2
k=1
;)=0

[XENSECP]

VOilà:

J'ai un exercice pour les limites et on me dit:

soient a,b et c des réels avec c=0. Soit f la fonction definie sur R\{-d/c}par : f(x)=(ax+b)/cx+d

determiner des réels , et k tels que f(x)=;)+(k/(x-;))

Mais des réels sont des nombres, noms? alors comment faire sans un seul chiffre ?
je suis perdu et personne dans mon entourage n'a réussis à m'aider.

Mets tout au même dénominateur (dans la 2ème expression) et tu pourras identifier les coefficients. Car contrairement à ton calcul et comme l'a dit laya, tu ne dois pas poser des valeurs pour a,b,c,d. Tu dois justement déterminer en fonction de a,b,c,d.

[Sylviel]

Edit : je n'avais pas vu que tu répondais au message précédent :mur: Je laisse quand même la suite du message au cas où...

a,b,c et d sont des paramètres. C'est à dire des nombres que tu connais. Tu peux imaginer que a vaut 3 ou 4... En revanche lambda, k et et mu sont des inconnues, donc des nombres que tu dois déterminer... Tu dois donc écrire
lambda = ...
k = ...
mu = ...

Avec dans les ... des a des b des c et des d.

[laya]

Ok Roneila, bonne réponse.

Si on prend une fonction qui a la même tête mais avec des valeurs de a, b, c et d différentes, on va toujours pouvoir changer son visage comme dans l'exemple. C'est pour ça qu'on va le faire en général, sans dire que a = machin , b = bidule, etc.

Il y a plusieurs façons de s'y prendre. Je te mets sur la piste de la première (la moins naturelle mais la plus rapide), on verra une autre par la suite :

On va d'abord changer le visage du numérateur :
Tu dois trouver deux nombres tels que pour tout x dans le domaine de définition de f :

Tu peux par exemple développer le membre de droite et utiliser le fait que cette égalité doit être vraie pour tous les nombres x du domaine de définition de f (c'est à dire une infinité).

[Roneila]

Alors

Pour ce qu'a dit XENSEPR
ça donne (ax+b)/(cx+d)=(;)x-;);)+k)/(x-;)) ?????

pour ce que dit sylvil
a=;)
b=c=k
d=;)

EN revanche pour laya,je suis encore moins sur:

ax+b=cx;)²d+;) <-- ça me parait bizare
dans ce cas ;)=b

[XENSECP]

Il faut d'abord transformer un peu l'expression pour pouvoir vraiment identifier :


Normalement et se déduisent immédiatement... reste juste k.

[laya]

EN revanche pour laya,je suis encore moins sur:

ax+b=cx;)²d+;) <-- ça me parait bizare
dans ce cas =b

On a pour tout x dans l'ensemble de définition de f :

Pour que cela soit vrai pour tout x dans l'ensemble de définition de f, il faut et il suffit que :



ça donne tout de suite :




Ce qui va te permettre de résoudre ton exo en une ligne supplémentaire.

Remarque :
On aurait pu décrire tout ça une ligne comme suit, mais il est mieux que tu comprennes d'où viennent les choses au lie des les parachuter :
Voici:

[Roneila]

merci

donc pour mon exercice, ça donne:
;)= a/c
;)= -d/c
et k=b/c

[XENSECP]

merci

donc pour mon exercice, ça donne:
= a/c
= -d/c
et k=b/c

Les 2 premiers c'est bon. Mais je t'ai dit de faire attention pour k (ce que tu n'as pas fait) donc c'est faux.

[laya]

merci

donc pour mon exercice, ça donne:
= a/c
= -d/c
et k=b/c

Si tu avais lu la réponse juste au dessus de ton dernier message !