[complexes]Demontrer que c'est un imaginaire pur
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 14 Oct 2009, 18:44
par jklmmlkj » 14 Oct 2009, 18:44
Bonjour tout le monde, je voudrais démontrer que (1+z)/(1-z) est un imaginaire pur mais je n'arrive pas... Je voulais essayer la propriété zbarre = -z mais je ne vois pas trop comment m'y prendre vu qu'on a pas l'expression de z...
Merci de vos réponses!
-
dudumath
- Membre Relatif
- Messages: 417
- Enregistré le: 18 Nov 2007, 11:04
-
 par dudumath » 14 Oct 2009, 18:46
par dudumath » 14 Oct 2009, 18:46
tu peux poser z=x+iy, et multiplier par le conjugué du dénominateur au numérateur et au dénominateur, après ca va tout seul...
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 14 Oct 2009, 19:19
par jklmmlkj » 14 Oct 2009, 19:19
Merci mais je ne me retrouve pas avec un imaginaire pur, j'ai :
(1-x²-y²)/(1-2x+x²+y²)+i(2y)/(1-2x+x²+y²)
La partie réelle n'est pas nul...
J'ai pourtant fait : ((1+x)+iy)((1-x)+iy)/((1-x)-iy)((1-x)+iy)
Merci d'avance!

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 14 Oct 2009, 19:25
par Ericovitchi » 14 Oct 2009, 19:25
(1+z)/(1-z) imaginaire pur quelque soit z ?
non, il suffit de faire z=0 pour tomber sur un réel
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 14 Oct 2009, 19:29
par jklmmlkj » 14 Oct 2009, 19:29
J'ai oublié de préciser que |z| = 1 et z différent de 1...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 14 Oct 2009, 19:38
par Ericovitchi » 14 Oct 2009, 19:38
si |z|=1 poses

utilises le fait que

et

et

pour simplifier l'expression. Mais tu ne tombes pas sur un imaginaire pur
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 14 Oct 2009, 19:40
par wserdx » 14 Oct 2009, 19:40
Bah, dans ce cas
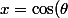, y=\sin(\theta))
Remplace dans ta formule, et tu devrais trouver que ta partie réelle s'annule.
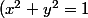)
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 14 Oct 2009, 19:42
par jklmmlkj » 14 Oct 2009, 19:42
ok, merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
