Bonsoir sinderalla,
On peut appliquer THALES dans le triangle CEB.
O milieu de CE et I milieu de CB => OI//BE
Toujours THALES dans le triangle FEB
J milieu de EF et O' milieu de FB => JO'//BE
De OI//BE et JO'//BE on déduit que OI//JO'
Toujours THALES dans le triangle BCF
I milieu de CB et O' milieu de FB => O'I//CF
Toujours THALES dans le triangle ECF
O milieu de EC et J milieu de EF => OJ//CF
De O'I//CF et OJ//CF on déduit que O'I//OJ
Comme on montré OI//JO' et O'I//OJ, on en déduit que IOJO' est un parallelogramme.
On a demontré BE perpendiculaire à CF dans les questions précedentes.
OI//BE et O'I//CF, donc OI prependiculaire à O'I.
IOJO' est donc un rectangle.
Il faut démontrer maintenant que IO'=OI

=
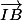
+

= (
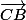
+
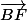
)/2 =
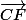
/ 2
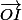
=
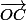
+
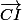
= (
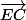
+
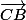
)/2 =
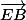
/ 2
B est l'image de F par la rotation de centre A et d'angle Pi/2.
E est l'image de C par la rotation de centre A et d'angle Pi/2.
La rotation conservant les distances on a démontré que CF = EB
Donc IO' = OI, d'où finalement IOJO' est un carré
L'aire du carré = OI² = CF²/4



