Complexe dans un repère orthonormé
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
loustak
- Messages: 6
- Enregistré le: 13 Fév 2015, 08:23
-
 par loustak » 21 Fév 2015, 18:01
par loustak » 21 Fév 2015, 18:01
Bonjour,
J'ai un DM à faire.
Voici la première question sur la quel je bloque :
Le plan complexe est rapporté à un repère orthonormé (0, u, v), d'unité graphique 1 cm. On note i le nombre complexe de module 1 et d'argument pi/2
Placer dans ce plan les points A, B et C d'affixe respectives za = -4; zb = -2 + 2i; zc = -2 -2i
Ce que j'ai fait : j'ai tracé un repère avec à 1 cm de l'axe x j'ai mis u et à 1 cm de l'axe y j'ai mis v. Cependant je ne parviens pas à placer les points. Comment dois-je m'y prendre ?
Faut-il faire des calculs ?
Merci de votre aide.
-
loustak
- Messages: 6
- Enregistré le: 13 Fév 2015, 08:23
-
 par loustak » 21 Fév 2015, 18:10
par loustak » 21 Fév 2015, 18:10
Bon j'ai enfait réussi à placer mes points. J'obtiens un triangle isocèle.
Maintenant je bloque à la question B :
écrire sous la forme re exposant (i phi) ou r est un nombre réel strictement positif et phi un nombre réel compris entre -pi et pi.
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 21 Fév 2015, 18:11
par paquito » 21 Fév 2015, 18:11
loustak a écrit:Bonjour,
J'ai un DM à faire.
Voici la première question sur la quel je bloque :
Ce que j'ai fait : j'ai tracé un repère avec à 1 cm de l'axe x j'ai mis u et à 1 cm de l'axe y j'ai mis v. Cependant je ne parviens pas à placer les points. Comment dois-je m'y prendre ?
Faut-il faire des calculs ?
Merci de votre aide.
A(-4; 0), B(-2; 2), C(-2; -2)

,

, etc...
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 21 Fév 2015, 18:12
par Manny06 » 21 Fév 2015, 18:12
loustak a écrit:Bonjour,
J'ai un DM à faire.
Voici la première question sur la quel je bloque :
Ce que j'ai fait : j'ai tracé un repère avec à 1 cm de l'axe x j'ai mis u et à 1 cm de l'axe y j'ai mis v. Cependant je ne parviens pas à placer les points. Comment dois-je m'y prendre ?
Faut-il faire des calculs ?
Merci de votre aide.
ZA=-4 donc A a pour coordonnées (-4;0)
ZB=-2+2i donc B a pour coordonnées (-2;2)
-
loustak
- Messages: 6
- Enregistré le: 13 Fév 2015, 08:23
-
 par loustak » 21 Fév 2015, 18:17
par loustak » 21 Fév 2015, 18:17
Merci de vos réponses j'ai réussi. Maintenant on me demande d'écrire zb et zc sous la forme re(exposant i * phi) dans la quel r est un nombre réel strictement positif et phi un nombre réel compris entre pi et -pi.
Je ne comprend pas vraiment comment. Dans le cours on à la même formule pour la forme exponentielle je ne sais pas si cela à un rapport...
-
loustak
- Messages: 6
- Enregistré le: 13 Fév 2015, 08:23
-
 par loustak » 21 Fév 2015, 18:21
par loustak » 21 Fév 2015, 18:21
J'ai du mal à voir d'ou sort le
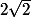
et le
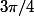
J'essaye de faire la même chose pour zc du coup ce serais

?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 21 Fév 2015, 18:36
par Manny06 » 21 Fév 2015, 18:36
loustak a écrit:J'ai du mal à voir d'ou sort le
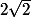
et le
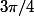
J'essaye de faire la même chose pour zc du coup ce serais

?
tu dois chercher le module et l'argument du complexe
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 22 Fév 2015, 09:47
par paquito » 22 Fév 2015, 09:47
Manny06 a écrit:ZA=-4 donc A a pour coordonnées (-4;0)
ZB=-2+2i donc B a pour coordonnées (-2;2)
Je vais détailler pour
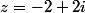
sachant que
+isin(\theta)=e^{i\theta})
le module de
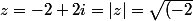^2+2^2}=\sqrt{8}=2\sqrt{2})
;
on va écrire z sous la forme
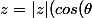+isin(\theta))
;
ça donne
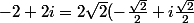=)
+isin(\frac{3\pi}{4}))=2\sqrt{2}e^{\frac{3i\pi}{4}})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
