Complement de fonction derivéé !!

par **fiofio34** » 13 Oct 2013, 09:25

bonjour , j'ai un dm de math et j'aimerai un peu d'aide
On me demande ça :
Determiner la derivee puis le tableau d variation des deux fonctions suivante definies sur I.
1. f(x)=Vx²+x+1 avec I=reel
2. g(x)=(3x²-1)exposant 3 avec I= reel
j'ai deja derivee mais je n'arrive pas a faire les tableaux
Pour f(x) je trouve 2x+1/V x²+x+1 et g(x) je trouve 18x (3x-1)²

par **SaintAmand** » 13 Oct 2013, 09:34

fiofio34 a écrit:bonjour , j'ai un dm de math et j'aimerai un peu d'aide
On me demande ça :
Determiner la derivee puis le tableau d variation des deux fonctions suivante definies sur I.
1. f(x)=Vx²+x+1 avec I=reel
2. g(x)=(3x²-1)exposant 3 avec I= reel
j'ai deja derivee mais je n'arrive pas a faire les tableaux
Pour f(x) je trouve 2x+1/V x²+x+1 et g(x) je trouve 18x (3x-1)²

Ne vois-tu pas que tes notations sont illisibles ? Dans Vx+1 il faut comprendre

ou

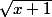
? Utilise sqrt pour la racine carrée, et ^ pour les puissances comme sur ta calculatrice. Cela donne donc f(x) = sqrt(x^2+x+1).

Enfin je te conseille de revoir les règles de priorité vues en cinquième. En particulier, la multiplication et la division sont prioritaires sur l'addition et la soustraction.

par **fiofio34** » 13 Oct 2013, 09:43

1. f(x)= /sqrt{x²+x+1} avec I=reel
2. g(x)=(3x^2-1)^3 avec I= reel
j'ai deja derivee mais je n'arrive pas a faire les tableaux
Pour f(x) je trouve 2x+1/ /sqrt{ x²+x+1 }et g(x) je trouve 18x (3x^2-1)²

par **SaintAmand** » 13 Oct 2013, 09:56

Pour f(x) je trouve 2x+1/ /sqrt{ x²+x+1 }et g(x) je trouve 18x (3x-1)²

Oh là, là, je plains ton prof :-)

Pourquoi n'écris-tu pas f'(x) = 2x+1/sqrt(x^2+x+1) ?

En tout cas, tes dérivées sont toutes les deux fausses. Relis tes formules, et refais les exemples et exercices de ton cours.

par **fiofio34** » 13 Oct 2013, 10:33

les formules sont u'(x) / 2sqrtu(x) et nu'(x)X(u(x))^n-1

par **fiofio34** » 13 Oct 2013, 11:13

je ne vois donc pas pourquoi mes derivees sont fausses

par **coote** » 13 Oct 2013, 11:20

fiofio34 a écrit:je ne vois donc pas pourquoi mes derivees sont fausses

si, tu n'a pas applique correctement la formule pour f

par **SaintAmand** » 13 Oct 2013, 11:21

fiofio34 a écrit:les formules sont u'(x) / 2sqrtu(x) et nu'(x)X(u(x))^n-1

Non. Voici ce que tu as écris:

et

.

La dérivée de sqrt(u) est u'/(2sqrt(u)) et la dérivée de u^n est nu'u^(n-1).

Note les parenthèses.

par **fiofio34** » 13 Oct 2013, 11:26

u'(x)/(2sqrtu(x)) et nu'(x)((u(x))^(n-1) c mieux ?!

par **SaintAmand** » 13 Oct 2013, 11:35

fiofio34 a écrit:u'(x)/(2sqrtu(x)) et nu'(x)((u(x))^(n-1) c mieux ?!

Oui, c'est ce que j'ai écris. Tu n'as plus qu'à les appliquer correctement et à écrire le résultat en n'oubliant pas les parenthèses quand elles sont nécessaires.

par **fiofio34** » 13 Oct 2013, 11:39

2x+1/(2sqrtu(x^2+x+1)) et 3X6x((3x^2-1))^(2)=18x((3x^2-1))^2

par **fiofio34** » 13 Oct 2013, 11:55

les resultats je les ai depuis le debut , mais je ne sais juste pas comment faire les tableaux c'est tout

par **SaintAmand** » 13 Oct 2013, 12:28

fiofio34 a écrit:les resultats je les ai depuis le debut , mais je ne sais juste pas comment faire les tableaux c'est tout

NON. La dérivée de f est mal écrite (il manque des parenthèses), et celle de g est fausse.

par **fiofio34** » 13 Oct 2013, 12:35

je suis desolé mais la derivée de f est correcte ! f'(x)= (2x+1)/2sqrt((x^2+x+1))
et g(x) n'a pas de raison d'etre fausse car j'ai replacer n par 3 ; u'(x) par 6x et (u(x)) par (3^2 -1) et n-1 par ^2

par **SaintAmand** » 13 Oct 2013, 12:48

fiofio34 a écrit:je suis desolé mais la derivée de f est correcte ! f'(x)= (2x+1)/2sqrt((x^2+x+1))

Tu insistes ! Maintenant elle l'est.

et g(x) n'a pas de raison d'etre fausse car j'ai replacer n par 3 ; u'(x) par 6x et (u(x)) par (3^2 -1) et n-1 par ^2

Oui. N'aurais-tu pas réédité tes messages ?

Et maintenant, cela veut-dire quoi précisement quand tu dis que tu ne sais pas faire un tableau de signes ?

par **fiofio34** » 13 Oct 2013, 12:50

je ne les pas réédité !
je ne sait pas comment trouver les variations des fonctions , les etapes et quoi mettre dedans

par **SaintAmand** » 13 Oct 2013, 12:55

fiofio34 a écrit:je ne les pas réédité !

Menteur. Message de 10h43 corrigé à 12h09. Evidemment si tu corriges les erreurs tu peux toujours prétendre que j'ai tort. :-)

je ne sait pas comment trouver les variations des fonctions , les etapes et quoi mettre dedans

Fais un effort. Tu as un cours et un manuel dans lequel il y a tout plein d'exemples. On va quand même pas te refaire un cours parce que tu as la flegme de chercher. Donc regardes ton cours et reviens s'il y a un truc que tu piges pas.

par **fiofio34** » 13 Oct 2013, 12:59

moi j'ai trouvé que 2x+1 est croissant et 2sqrt((x^2+x+1)) decroissante sur ]-infini; -1] et croissante sur [-1;+infini[ et que g'(x) est derivable sur 18x((3x^2-1))^2 et derivable sur I

par **SaintAmand** » 13 Oct 2013, 13:12

fiofio34 a écrit:moi j'ai trouvé que 2x+1 est croissant et 2sqrt((x^2+x+1)) decroissante sur ]-infini; -1] et croissante sur [-1;+infini[ et que g'(x) est derivable sur 18x((3x^2-1))^2 et derivable sur I

Tu me donnes mal à la tête :-)

Il te faut d'abord étudier les signes des dérivées.

Ce sera plus pratique et certainement plus lisible si tu scannes ou photographies tes tableaux de variations.

Pour info, il n'est pas nécessaire d'utiliser les dérivées pour étudier les sens de variations de tes fonctions.

par **fiofio34** » 13 Oct 2013, 13:16

je dois etudier les variations de quoi exactement ?

Complement de fonction derivéé !!

complement de fonction derivéé !!

Qui est en ligne