Coefficient directeur et dérivabilité
15 messages
- Page 1 sur 1
Coefficient directeur et dérivabilité
Bonjour à tous, je travaille sur un exercice d'un dm qui porte sur la fonction exponentiel. Je n'ai aucun problème avec cette fonction, j'ai réussi l'exercice parfaitement, à lexception de la dernière question qui me pose une colle.
[CENTER]"4. Soient x un nombre réel non nul et les points M(x;f(x)) et M'(-x;f(-x)) de la courbe C.
a) Établir que f(-x) = x/(e^x)-1 puis déterminer le coefficiant directeur de la droite (MM').
b) On a admet la fonction f dérivable en 0. Que suggère alors le résultat précédent "
[/CENTER]
J'ai réussi la question 4.a), le coef. directeur est 1/2.
Mais j'ai du mal à cerner le rapport avec la dérivabilité en 0. Je suppose que ça doit suggérer l'existence d'une tengente à C en 0 mais je ne sais pas comment le prouver.
Pour donner plus de sens à ma question, je vous donne f(x)
[CENTER]f(x) = (xe^x) / ((e^x)-1) si x différent de 0.[/CENTER]
Je vous en serait reconnaissant si vous voulez bien m'aidez ! Merci =)
[CENTER]"4. Soient x un nombre réel non nul et les points M(x;f(x)) et M'(-x;f(-x)) de la courbe C.
a) Établir que f(-x) = x/(e^x)-1 puis déterminer le coefficiant directeur de la droite (MM').
b) On a admet la fonction f dérivable en 0. Que suggère alors le résultat précédent "
[/CENTER]
J'ai réussi la question 4.a), le coef. directeur est 1/2.
Mais j'ai du mal à cerner le rapport avec la dérivabilité en 0. Je suppose que ça doit suggérer l'existence d'une tengente à C en 0 mais je ne sais pas comment le prouver.
Pour donner plus de sens à ma question, je vous donne f(x)
[CENTER]f(x) = (xe^x) / ((e^x)-1) si x différent de 0.[/CENTER]
Je vous en serait reconnaissant si vous voulez bien m'aidez ! Merci =)
Bonjour ! Je pense que ce qui est demandé est la chose suivante. A priori, la fonction f n'est pas définie en 0, en tout cas pas par la formule que tu as indiquée. Mais on peut peut-être la prolonger en 0 (peut-être que dans l'énoncé, on précise f(0) = quelque chose, genre f(0) = 0, ce qui ne m'étonnerait pas).
Peut-être même que f est alors continue. Qu'elle soit continue en dehors de 0 ne pose pas de problème, mais qu'elle soit continue aussi en 0 n'est pas évident puisque ce n'est pas la même formule qui définit f en 0.
Et peut-être même que f est alors dérivable en 0. Bien sûr, on ne peut pas calculer la dérivée en 0 avec la formule f(x) = (xe^x) / ((e^x)-1) puisque celle-ci n'est valable qu'en dehors de 0. L'idée de cet exercice, c'est qu'on se souvient que la dérivée, c'est le coefficient directeur de la tangente, et qu'on obtient celui-ci en faisant la limite des droites (OM) (ou (OM')) lorsque M tend vers O (ou M' tend vers O), donc en fait la limite des droites (MM') lorsque M et M' tendent l'un vers l'autre. Or ici, cette limite est calculable car le coefficient directeur que tu as trouvé ne dépend pas de x (ce qui a dû te surprendre, non ?). (Je parle de limite de droite pour aider l'intuition, en fait il s'agit de limite de coefficient directeur.) Tout ça suggère que la dérivée en 0, qu'on suppose exister, vaut une certaine valeur que tu as peut-être déjà calculée...
Je ne sais pas si j'ai été clair. Je me refuse de te gâcher le plaisir de la découverte en faisant des calculs, du coup ce n'est pas facile d'expliquer l'idée de départ...
Peut-être même que f est alors continue. Qu'elle soit continue en dehors de 0 ne pose pas de problème, mais qu'elle soit continue aussi en 0 n'est pas évident puisque ce n'est pas la même formule qui définit f en 0.
Et peut-être même que f est alors dérivable en 0. Bien sûr, on ne peut pas calculer la dérivée en 0 avec la formule f(x) = (xe^x) / ((e^x)-1) puisque celle-ci n'est valable qu'en dehors de 0. L'idée de cet exercice, c'est qu'on se souvient que la dérivée, c'est le coefficient directeur de la tangente, et qu'on obtient celui-ci en faisant la limite des droites (OM) (ou (OM')) lorsque M tend vers O (ou M' tend vers O), donc en fait la limite des droites (MM') lorsque M et M' tendent l'un vers l'autre. Or ici, cette limite est calculable car le coefficient directeur que tu as trouvé ne dépend pas de x (ce qui a dû te surprendre, non ?). (Je parle de limite de droite pour aider l'intuition, en fait il s'agit de limite de coefficient directeur.) Tout ça suggère que la dérivée en 0, qu'on suppose exister, vaut une certaine valeur que tu as peut-être déjà calculée...
Je ne sais pas si j'ai été clair. Je me refuse de te gâcher le plaisir de la découverte en faisant des calculs, du coup ce n'est pas facile d'expliquer l'idée de départ...
salut
sans parler même de continuité (même si ça pose un problème car pour être dérivable il faut être continue et même exister) mais tout de même ... il serait donc bien d'avoir toutes les questions !!!!
lorsque x tend vers 0 alors la droite (MM') tend vers la "tangente à la courbe de f au point d'abscisse 0"
sans parler même de continuité (même si ça pose un problème car pour être dérivable il faut être continue et même exister) mais tout de même ... il serait donc bien d'avoir toutes les questions !!!!
lorsque x tend vers 0 alors la droite (MM') tend vers la "tangente à la courbe de f au point d'abscisse 0"
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Robic a écrit:Oui, mais comme l'a dit chan79, on ne demande pas de démonstration. À mon avis il faut rester au niveau intuitif. (Et j'approuve totalement qu'on pose ce genre de question dans un devoir de lycée !)
On peut montrer que f'(0)=1/2 avec la règle de L'Hôpital ou un DL mais au niveau lycée, il s'agit sans doute de visualiser la position limite de (MM') quand M se rapproche de (0,1)
Voilà. Et ce que j'aime bien dans cette question, c'est que pour répondre, il faut garder en tête la définition de la dérivée vue comme coefficient directeur de la tangente (puisqu'il faut deviner comment va se placer cette tangente), donc garder en tête une vision, heu... visuelle de la dérivée. Je trouve ça plus intéressant que de juste utiliser des formules.
Robic a écrit:Voilà. Et ce que j'aime bien dans cette question, c'est que pour répondre, il faut garder en tête la définition de la dérivée vue comme coefficient directeur de la tangente (puisqu'il faut deviner comment va se placer cette tangente), donc garder en tête une vision, heu... visuelle de la dérivée. Je trouve ça plus intéressant que de juste utiliser des formules.
écrit et approuvé par Robic .... :ptdr: je plaisante bien sur
donc la seule et unique réponse qui convienne est ma première réponse ....
augmentée de :: et donc f'(0) = 1/2
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
certes avec un point de rebroussement ....
mais si on prend par exemple la fonction définie par ::
 = \sqrt x) si
si 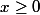
 = -\sqrt {-x}) si
si 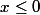
alors f n'est pas dérivable en 0 mais la droite (MN) tend vers la tangente à la courbe de f au point d'abscisse 0
avec M(x, f(x)) et N(-x, f(-x))
:lol3:
mais si on prend par exemple la fonction définie par ::
alors f n'est pas dérivable en 0 mais la droite (MN) tend vers la tangente à la courbe de f au point d'abscisse 0
avec M(x, f(x)) et N(-x, f(-x))
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
