Chiffre d'Affaire d'un hôtel - Régression linéaire
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 19 Fév 2021, 17:58
par novicemaths » 19 Fév 2021, 17:58
Bonsoir

La droite de régression est:
-2,398489276d + 777,792475Le coefficient de corrélation est;
-0,9326695229Avec ces données je ne vois pas comment déterminer l'expression du chiffre d'affaire et le prix optimal du chiffre d'affaire.
A bientôt
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 20 Fév 2021, 11:16
par lyceen95 » 20 Fév 2021, 11:16
Indice 1 : Quelle est la définition du Chiffre d'affaire.
Ou bien
Indice 1bis : Quand le prix est de 85 Euros, et que j'ai 518 clients, quel est mon chiffre d'affaire ?
Indice n°2 : quand le prix est de d et que le nombre de clients est -2,398489276d + 777,792475 , quel est mon chiffre d'affaire ?
Question : Pour quelle valeur de d ce chiffre d'affaire est il maximal ?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 20 Fév 2021, 17:24
par novicemaths » 20 Fév 2021, 17:24
Bonsoir
Si le prix d'une nuit est 85 € avec 518 clients on fait 85 x 518 = 44030
Le chiffre d'affaire est D.
Normalement la valeur de d=278
A bientôt
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 15 Fév 2022, 20:51
par novicemaths » 15 Fév 2022, 20:51
Bonsoir
Je n'arrive toujours pas à calculer le prix optimal.
J'ai trouvé cette expression
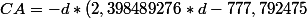)
Je cherche le prix optimal.
A bientôt
-
catamat
- Habitué(e)
- Messages: 1368
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 18 Fév 2022, 14:53
par catamat » 18 Fév 2022, 14:53
On a un trinôme du type ax²+bx+x avec a<0
On sait qu'il admet un maximum en
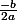
ou alors chercher la dérivée...
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 19 Fév 2022, 01:35
par novicemaths » 19 Fév 2022, 01:35
Bonjour
Voici les calculs dans le détaille.
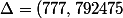^2 -4 \times (-2,398489276 \times 0)=(777,792475)^2 -4 \times 0= 604961,134166625625)
}= \frac{-1555,58495}{-4,796978552} =324,28432463001764949313035827807)
=27564,167593551500206916080453636)
€
Est-ce que j'ai trouvé le prix optimal ?
A bientôt
-
catamat
- Habitué(e)
- Messages: 1368
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 19 Fév 2022, 14:21
par catamat » 19 Fév 2022, 14:21
Hélas non !
Là, vous cherchez d pour que le chiffre d'affaires soit nul ! En fait, en 0 et en -b/a.
Le maximum est en -b/(2a) soit exactement la moitié de la valeur d1 que vous trouvez.
Explications :
Si on appelle f la fonction telle que f(x)=ax²+bx+c
sa dérivée f' est telle que f'(x)=2ax+b
Elle s'annule en -b/(2a), est du signe de a (donc négative) à droite de -b/(2a), et donc positive à gauche.
f présente bien un maximum en -b(2a)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités

