Un carré n'est jamais égal à 3 modulo 4 : preuve

par **Grizet** » 09 Aoû 2016, 16:10

Bonjour, tout est dans le titre.
Ce que j'ai essayé :
Soit

un carré. Il est donc égal à

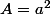
L'idée est de résoudre l'équation :

Resolvons !

Autrement dit :

. Donc,

. Et donc pas de contradiction ....

Et là je suis bloqué

par **Grizet** » 09 Aoû 2016, 16:14

Donc

est multiple de 4.

par **Grizet** » 09 Aoû 2016, 16:15

Donc, je suppose qu'il faut résoudre... mais comment ?

par **anthony_unac** » 09 Aoû 2016, 16:40

Bonjour,

Une façon de faire consiste à séparer les cas ou

est pair et ou

est impair.
Sachant que

est pair alors il peut se réécrire sous la forme : ......
En élevant cette forme au carré, il vient .......
La suite, c'est vous qui allez me la donner très certainement

par **Grizet** » 09 Aoû 2016, 18:10

Si a pair :

impossible car dans Z
SI à impair :

. Il faut factoriser peut être ?

par **anthony_unac** » 09 Aoû 2016, 18:16

Vous allez trop vite, reprenons :
Sachant que

est pair alors il peut se réécrire sous la forme :

(il manque 2 caractères)
En élevant cette forme au carré, il vient .......

par **samoufar** » 09 Aoû 2016, 18:25

Bonjour,

Avant de distinguer les cas, on peut remarquer que si

est un multiple de 4, alors

est pair, donc

et a fortiori

est impair.

Ensuite, il reste à poser

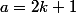
comme a dit anthony_unac et ça devrait marcher

par **Pseuda** » 09 Aoû 2016, 18:55

Grizet a écrit:Bonjour, tout est dans le titre.
Ce que j'ai essayé :
Soit un carré. Il est donc égal à

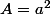
L'idée est de résoudre l'équation :
Resolvons !

Autrement dit : . Donc, . Et donc pas de contradiction ....

Et là je suis bloqué

Bonsoir,

Si tu ne veux pas t'embêter, tu peux aussi établir une table de congruence modulo 4 :
Selon que

. Peut-on avoir

?

par **zygomatique** » 09 Aoû 2016, 19:02

salut

oui la table de congruence ... j'ai failli intervenir et la proposer ...

sinon avec l'idée de pair impair tout simplement :

épictou ...

Grizet a écrit:Si a pair : impossible car dans Z
SI à impair : . Il faut factoriser peut être ?

faut surtout développer correctement ...

par **anthony_unac** » 09 Aoû 2016, 19:09

Quel dommage d'avoir écrit ces deux lignes à la place du gamin !
Je suis persuadé qu'il aurait été très heureux et très fier de trouver la solution par lui même mais à présent c'est foutu

par **zygomatique** » 09 Aoû 2016, 19:22

de toute façon il était parti sur une très mauvaise piste et avec une erreur ... voir la citation de grizet que je donne ...

par **Grizet** » 09 Aoû 2016, 20:34

Gamin ? C'est moi ou vous faites les malins ? Il me semble que c'est un peu lâche de parler derrière son écran ...

Enfin bref, j'ai trouvé ce que je cherchais, merci, bonne continuation.

Un carré n'est jamais égal à 3 modulo 4 : preuve

Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Re: Un carré n'est jamais égal à 3 modulo 4 : preuve

Qui est en ligne