Bonjour, je suis blocké est-ce que quelqu’un peut m’aider s il vous plait
lim x -> 0 (2x-sin(2x))/((2x)^2)
Calculer cette limite sans utiliser la règle de l hôpital
4 messages
- Page 1 sur 1
Re: Calculer cette limite sans utiliser la règle de l hôpita
Salut,
Déjà, je vois vraiment pas l'intérêt du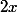 qui traîne partout dans ta limite : c'est évidement la même chose que
qui traîne partout dans ta limite : c'est évidement la même chose que }{x^2}) .
.
Ensuite, si tu ne veut pas utiliser ni la règle de la règle de L'Hôpital, ni développement limité ni quoi que ce soit qui ressemble de prés ou de loin à une des formules de Taylors, alors... il faut un peut réfléchir...
Une méthode très simple (seul prérequis : les tableaux de variation de fonctions), mais longue, c'est d'étudier les fonctions\!=\!x\!-\!\sin(x)\!+\!\lambda x^3) qui donnent
qui donnent \!=\!1\!-\!\cos(x)\!+\!3\lambda x^2\ ;\ f''(x)\!=\!\sin(x)\!+\!6\lambda x\ ; \ ;\ f'''(x)\!=\!\cos(x)\!+\!6\lambda) .
.
Si on a
on a \!\geq\!0) pour tout
pour tout  donc
donc 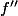 est croissante sur
est croissante sur  [tableau de variations de
[tableau de variations de 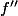 ]
]
Or\!=\!0) donc
donc  sur
sur 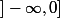 puis
puis  sur
sur 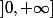 ce qui signifie que
ce qui signifie que  est décroissante puis croissante avec un minimum en
est décroissante puis croissante avec un minimum en 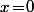 [tableau de variations de
[tableau de variations de  ].
].
Or\!=\!0) donc
donc  sur
sur  ce qui signifie que
ce qui signifie que  est croissante sur
est croissante sur  [tableau de variations de
[tableau de variations de  ].
].
Et comme\!=\!0) , ça signifie que
, ça signifie que  sur
sur 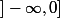 puis que
puis que  sur
sur 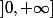 c'est à dire que
c'est à dire que \!\leq\!-\frac{1}{6}x^3) pour
pour  et que
et que \!\geq\!-\frac{1}{6}x^3) pour
pour  .
.
Même raisonnement avec qui donne
qui donne \!\leq\!0) pour tout
pour tout  et qui permet à terme d'obtenir d'autres inégalité concernant
et qui permet à terme d'obtenir d'autres inégalité concernant ) .
.
Et avec les encadrements obtenus, tu conclue facilement concernant la limite en question.
Déjà, je vois vraiment pas l'intérêt du
Ensuite, si tu ne veut pas utiliser ni la règle de la règle de L'Hôpital, ni développement limité ni quoi que ce soit qui ressemble de prés ou de loin à une des formules de Taylors, alors... il faut un peut réfléchir...
Une méthode très simple (seul prérequis : les tableaux de variation de fonctions), mais longue, c'est d'étudier les fonctions
Si
Or
Or
Et comme
Même raisonnement avec
Et avec les encadrements obtenus, tu conclue facilement concernant la limite en question.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Calculer cette limite sans utiliser la règle de l hôpita
C est un tout petit peu long mais cv j ai compris votre raisonnement, Merci beaucoup pour votre temps.
Sinon existe-t-il une méthode plus courte ?
Sinon existe-t-il une méthode plus courte ?
Re: Calculer cette limite sans utiliser la règle de l hôpita
Pour }{x^2}) qui ressemble un peu à ton truc, y'a l'astuce classique de multiplier le numérateur et le dénominateur par
qui ressemble un peu à ton truc, y'a l'astuce classique de multiplier le numérateur et le dénominateur par ) , mais là je vois pas bien comment faire.
, mais là je vois pas bien comment faire.
Bref, en utilisant uniquement les outils "standard" du Lycée, à froid, je vois pas d'autre truc que celui que je t'ai proposé ci dessus.
Bref, en utilisant uniquement les outils "standard" du Lycée, à froid, je vois pas d'autre truc que celui que je t'ai proposé ci dessus.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
