Calcul d'une limite svp
14 messages
- Page 1 sur 1
Re: Calcul d'une limite svp
Bonjour
Pour tout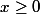 on a
on a 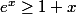
Donc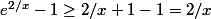
et alors\geq x\sqrt{\frac{2}{x}}=2\sqrt{x})
d'où la limite et + l'infini
J'avais vu le message de FBLP : j'ai donné une façon de répondre mais il faut voir ce qui propose....
Pour tout
Donc
et alors
d'où la limite et + l'infini
J'avais vu le message de FBLP : j'ai donné une façon de répondre mais il faut voir ce qui propose....
Re: Calcul d'une limite svp
Comme je l'ai posée tu obtiens le cas classique du :
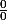
Et tu peux appliquer le théorème de Bernoulli-l'Hospital
Et tu peux appliquer le théorème de Bernoulli-l'Hospital
Re: Calcul d'une limite svp
Mais le prof interdit cette methode, est ce qu'il ya une aure méthode pour résoudre la limite ? svp
Re: Calcul d'une limite svp
Mais le prof interdit cette methode, est ce qu'il ya une aure méthode pour résoudre la limite ? svp
Re: Calcul d'une limite svp
Rebonjour
C'est tout de même bizarre: FBLP te propose d'utiliser la notion de dérivée (la règle de l'hospital c'est rien d'autre) et moi je te propose une minoration. Alors autre chose??
Quelque part on peut toujours utiliser la règle de l'hôpital sans citer le nom:
On a/(2/x)) qui tend vers 1 quand x tend +infinity
qui tend vers 1 quand x tend +infinity
Car (e^u-1)/u tend vers 1 quand u tend vers 0. (voir la dérivée de l'exponentielle, c'est la règle de l'hospital ds un cas particulier mais on s'en fout de le savoir ou pas).
Tu passe à la racine....
Avec ça tu as la réponse.
C'est tout de même bizarre: FBLP te propose d'utiliser la notion de dérivée (la règle de l'hospital c'est rien d'autre) et moi je te propose une minoration. Alors autre chose??
Quelque part on peut toujours utiliser la règle de l'hôpital sans citer le nom:
On a
Car (e^u-1)/u tend vers 1 quand u tend vers 0. (voir la dérivée de l'exponentielle, c'est la règle de l'hospital ds un cas particulier mais on s'en fout de le savoir ou pas).
Tu passe à la racine....
Avec ça tu as la réponse.
Re: Calcul d'une limite svp
Pour la limite en 0+
Je commencerai par me débarrasser de la racine carrée (la fonction est>0.
f(x)^2=x^2( exp(2/x)-1)=x^2 exp(2/x)-x^2=[xexp(1/x)]^2-x^2
x^2 tend vers 0.
On regarde donc la limite de xexp(1/x). En posant x=1/u on
a xexp(1/x)=exp(u)/u avec u qui tend vers +ìnfty.
C'est connu que exp(u)/u tend vers + infty.
On alors f(x)^2 tend vers +infty et dc f(x) aussi
Je commencerai par me débarrasser de la racine carrée (la fonction est>0.
f(x)^2=x^2( exp(2/x)-1)=x^2 exp(2/x)-x^2=[xexp(1/x)]^2-x^2
x^2 tend vers 0.
On regarde donc la limite de xexp(1/x). En posant x=1/u on
a xexp(1/x)=exp(u)/u avec u qui tend vers +ìnfty.
C'est connu que exp(u)/u tend vers + infty.
On alors f(x)^2 tend vers +infty et dc f(x) aussi
Re: Calcul d'une limite svp
zerow2001 a écrit:Mais le prof interdit cette methode, est ce qu'il ya une aure méthode pour résoudre la limite ? svp
Ce mathématicien a établit quelques chose de génial et on demande aux élèves en phase d'apprentissage de mettre de côté ce théorème extrêmement puissant,dont son utilité permet de réduire considérablement les calculs .On n 'a pas le droit de faire cela, ne serait ce que pour cet homme qui a marqué l'histoire des mathématiques!
sinon en cherchant autre chose, on reconnaît une différence de deux carrés
pour
on a,
comme, (à prouver c 'est facile)
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
