Calcul d'un arc sans angle et centre.

[lipsou]

Bonjour à tous.
Petit nouveau sur ce forum.
je suis serrurier travaillant sur des chantiers de restauration de bâtiments anciens.

Avec un tailleur de pierre nous sommes face à un problème.

Comment calculer un arc de cercle en n'ayant que la flèche et la distance entre A et B (soit le début et la fin de l'arc
Par le tracé nous avons une réponse, nous nous demandions si par l'algèbre il était possible de trouver un résultat.

:mur:

distance AB = 40
flèche = 10

Pardonnez moi mais je n'ai pas réussi à charger un croquis.... :cry:

[Monsieur23]

Aloha,

Il y a une formule permettant de retrouver le rayon du cercle en fonction de la corde et de la flèche de ton arc :

(où c est la longueur de la corde, f la longueur de la flèche)

Si tu trouves le rayon, tu peux placer le centre. Si tu connais le centre et le rayon, tu peux trouver l'angle au centre, donc la longueur de l'arc.

Edit : sauf erreur de calcul, je trouve une longueur d'arc d'environ 46.5

[Black Jack]

R = (4f² + AB²)/(8f) = (4*10² + 40²)/(8*10) = 25 (rayon du cercle)

Avec alpha l'angle au centre sous-tendant la corde, on a :

AB/2 = R.sin(alpha/2)
sin(alpha/2) = AB/(2R) = 40/50 = 0,8 ---> alpha/2 = arcsin(0,8) = 53,13°

alpha = 2*53,13 = 106,26°

Rayon du cercle : 25 (unités de longueur)
angle au centre sous tendant la corde : 106,26°

Longueur de l'arc = 2*arsin(0,8) * R = 46,36 (unités de longueur)

:zen:

[lipsou]

Merci beaucoup à tous pour votre aide!! :we: :we:

[mathelot]

pareil=2*25*arctan(4/3)=46.36

[Julien51]

Bonjour la formule pour calculer l'angle ? je ne m'en souvient plus (honte à moi).

J'ai juste un rayon (R13) et il me faut la longueur d'arc

[GaBuZoMeu]

Bonjour,

Peux-tu être plus explicite ? Tu connais sûrement autre chose que le rayon du cercle qui porte l'arc. Si c'est la seule information, ça va être un peu difficile de calculer la longueur de l'arc !

[Julien51]

Voici une image (prise avec lightshot) de mon plan avec entouré en rouge la partie que je veux calculer : http://prntscr.com/nutwqr

[GaBuZoMeu]

Le schéma n'est pas super précis sur la nature de l'arc de cercle. On a l'impression qu'il s'agit d'une moitié d'arc de cercle de flèche 1.5 et de rayon 13. Tu confirmes ? Si c'est le cas, la demi-corde sous le demi-arc de cercle est , soit un peu plus de 6.

[Julien51]

oui la corde sous l'arc est de 6 mais l'arc fait plus que 6 non ? http://prntscr.com/nuusn7 (photo plus zoomer)

[GaBuZoMeu]

Le demi-arc correspond à un angle 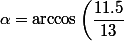et sa longueur est ( exprimé en radians, bien sûr).

[danyL]

la formule pour calculer l'angle ?

bjr
on peut calculer l'angle avec sa tangente
le côté opposé à l'angle est la demi-corde
le côté adjacent est la verticale de 11.5

ensuite avec l'angle tu peux déduire la longueur de l'arc


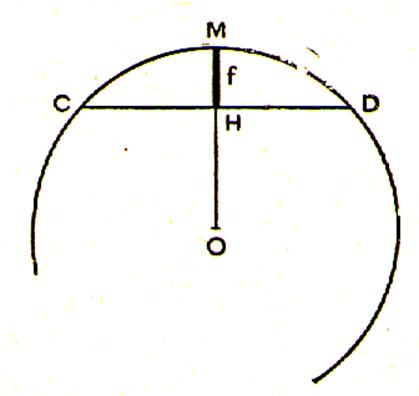
avec les notations de ce dessin ça donne :
tg (OH, OD) = HD / OH