bonjour,
pouvez-vous me donner un autre exemple sur l'integration par parties en utilisant la même methode que pour ce cours qui est pas mal fait :
cours ici
Car malgré que le cours soit bien expliquée, je trouve qu'il est difficile de bien comprendre du fait qu'il utilise une fonction exponentielle qui ne change pas lorsque que l'on la derive ou primitive.
merci pour vos reponses.
:we:
Besoin de comprendre l'integration par parties
29 messages
- Page 1 sur 2 - 1, 2
par Nightmare » 07 Juin 2006, 12:44
Bonjour
Par exemple, pour calculer :
dx)
Il suffit d'écrire que=1\times ln(x))
En effet, en posant=1\Rightarrow u(x)=x et v(x)=ln(x)\Rightarrow v'(x)=\frac{1}{x})
on obtient par parties :
dx=\underbrace{x\times ln(x)}_{u(x).v(x)}-\Bigint \underbrac{x\times \frac{1}{x}}_{u(x).v'(x)}dx)
Soit finalement :
dx=xln(x)-x)
modulo constante
:happy3:
Par exemple, pour calculer :
Il suffit d'écrire que
En effet, en posant
Soit finalement :
:happy3:
par abel » 07 Juin 2006, 12:48
Déjà ça provient du fait que :
(uv)' = u'v + uv' et donc :
' - uv' = [uv] - \int uv')
En général c'est pratique pour les fonctions telles que sin, cos, exp() car en les dérivant ou intégrant plusieurs fois on retombe sur les meme fonctions qu'au départ, et dans plein d'autres cas aussi...
exemple :
dx = [x^{2}\sin(x)]_{0}^{\Pi} - \int 2x\sin(x)dx)
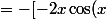]_{0}^{\Pi} + \int 2\cos(x)dx)
Ici la technique a été d'intégrer 2 fois par partie pour faire "disparaitre" le x²...De meme si on avait du x^n, il faudrait intégrer n fois par partie....
(uv)' = u'v + uv' et donc :
En général c'est pratique pour les fonctions telles que sin, cos, exp() car en les dérivant ou intégrant plusieurs fois on retombe sur les meme fonctions qu'au départ, et dans plein d'autres cas aussi...
exemple :
Ici la technique a été d'intégrer 2 fois par partie pour faire "disparaitre" le x²...De meme si on avait du x^n, il faudrait intégrer n fois par partie....
par Nightmare » 07 Juin 2006, 13:09
Edit moi même :
J'avais mal compris la remarque Mikou :lol3:
Non ça allait, mais heureusement que je passe en terminale ! :lol:
J'avais mal compris la remarque Mikou :lol3:
Non ça allait, mais heureusement que je passe en terminale ! :lol:
par fonfon » 07 Juin 2006, 13:14
Salut,
tu poses u(x)=lnx donc u'(x)=1/x
et v'(x)=x donc v(x)=x²/2
et tu appliques la formule...
tu poses u(x)=lnx donc u'(x)=1/x
et v'(x)=x donc v(x)=x²/2
et tu appliques la formule...
par Nightmare » 07 Juin 2006, 18:43
Une interressante :
Pour calculer.e^{x}dx)
On pose :=sin(x)\Rightarrow u'(x)=cos(x)\\v'(x)=e^{x}\Rightarrow v(x)=e^{x})
On obtient :
-\Bigint cos(x)e^{x}dx)
Interressons nous àe^{x}dx)
On pose :
=cos(x)\Rightarrow u'(x)=-sin(x)\\v'(x)=e^{x}\Rightarrow v(x)=e^{x})
Et on obtient :
e^{x}-\Bigint -sin(x)e^{x}dx)
soit encore :
e^{x}+I)
Finalement :
-cos(x)e^{x}-I)
ainsi :
-cos(x)))
Et pour finir :
-cos(x)))
modulo constante
:happy3:
Pour calculer
On pose :
On obtient :
Interressons nous à
On pose :
Et on obtient :
soit encore :
Finalement :
ainsi :
Et pour finir :
:happy3:
par Nightmare » 07 Juin 2006, 18:47
Messages croisés (j'ai modifié mon post en réponse à ta question)
:happy3:
:happy3:
par quaresma » 07 Juin 2006, 18:49
et si on reprenais mon exemple? :id:
juste pour voir ce que ca donnerai
juste pour voir ce que ca donnerai
par quaresma » 07 Juin 2006, 20:22
fonfon a écrit:Salut,
tu poses u(x)=lnx donc u'(x)=1/x
et v'(x)=x donc v(x)=x²/2
et tu appliques la formule...
comment fait-on pour determiner qui sera U ou qui sera V ?
par Nightmare » 07 Juin 2006, 20:23
Tu essayes de les déterminer afin que l'intégrande de la nouvelle intégrale obtenue après l'IPP soit primitivable facilement.
par quaresma » 07 Juin 2006, 20:25
Nightmare a écrit:Tu essayes de les déterminer afin que l'intégrande de la nouvelle intégrale obtenue après l'IPP soit primitivable facilement.
en francais ca donne quoi ? :doh:
par Nightmare » 07 Juin 2006, 20:28
La formule de l'IPP est :
S(u'v)=uv-S(uv')
Tu choisis u' et v afin que (uv') soit le plus facilement primitivable
Par exemple lors de mon calcul de 1*ln(x)
si j'avais pris v(x)=1 et u'(x)=ln( x ), pour procéder à l'IPP il faut calculer u(x), c'est à dire primitiver x->ln(x) ce qu'on cherche à faire à la base, donc ce choix ne serait pas judicieux
:happy3:
S(u'v)=uv-S(uv')
Tu choisis u' et v afin que (uv') soit le plus facilement primitivable
Par exemple lors de mon calcul de 1*ln(x)
si j'avais pris v(x)=1 et u'(x)=ln( x ), pour procéder à l'IPP il faut calculer u(x), c'est à dire primitiver x->ln(x) ce qu'on cherche à faire à la base, donc ce choix ne serait pas judicieux
:happy3:
29 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :