Besoin de comprendre l'integration par parties
29 messages
- Page 2 sur 2 - 1, 2
Non justement, on ne choisit pas U et V au hasard, il faut faire un choix judicieux comme je l'ai expliqué.
Le résultat en lui même ne sera pas différent que tu choisisses u et v différement étant donné qu'on calcule la même intégrale à la base, mais ce sera la facilité que tu auras à la calculer qui va différer :lol3:
Exemple :
Calculee^{x}dx) en posant
en posant =x+1\\v'(x)=e^{x}) puis refait le en posant
puis refait le en posant =e^{x}\\v'(x)=x+1)
Alors ? :lol3:
Le résultat en lui même ne sera pas différent que tu choisisses u et v différement étant donné qu'on calcule la même intégrale à la base, mais ce sera la facilité que tu auras à la calculer qui va différer :lol3:
Exemple :
Calcule
Alors ? :lol3:
Salut,
----
Des fois on est forcé à prendre des fonctions en dérivée ... par exemple : x*sin(x) , il est plus judicieux de prendre x et dérivé pour abaisser le degré.
il est de même lorsqu'il s'agit de ln(x) on est obligé de la prendre en dérivée car "on ne connais" pas de primitive direct.
----
Regard ici, il y a un exemple :
http://diverso.site.voila.fr/docs/sciences/maths/18.html
----
Des fois on est forcé à prendre des fonctions en dérivée ... par exemple : x*sin(x) , il est plus judicieux de prendre x et dérivé pour abaisser le degré.
il est de même lorsqu'il s'agit de ln(x) on est obligé de la prendre en dérivée car "on ne connais" pas de primitive direct.
----
Regard ici, il y a un exemple :
http://diverso.site.voila.fr/docs/sciences/maths/18.html
En gros retient ceci, en terminale tu en auras pas besoin de plus :
quand on a :
- polynome * (fonction chiante mais qui se primitive bien), on préfère poser U=polynome et V'=fonction chiante
(fonction chiante = {exp,sin,cos,sh,ch,fonction exprimée comme la dérivée d'une autre fonction...etc....})
- polynome*(fonction qu'on ne sait pas bien primitiver et qui se dérive bien), on préfère poser U = fonction..... et V'=polynome
ex : polynome * ln(x), on aime bien dériver ln(x) plutot que de le primitiver....
etc...j'espere que tu vois où je veux en venir.....
Bpon courage, il se peut qu'il y ait des exceptions mais en général on t'en demandera pas +....
quand on a :
- polynome * (fonction chiante mais qui se primitive bien), on préfère poser U=polynome et V'=fonction chiante
(fonction chiante = {exp,sin,cos,sh,ch,fonction exprimée comme la dérivée d'une autre fonction...etc....})
- polynome*(fonction qu'on ne sait pas bien primitiver et qui se dérive bien), on préfère poser U = fonction..... et V'=polynome
ex : polynome * ln(x), on aime bien dériver ln(x) plutot que de le primitiver....
etc...j'espere que tu vois où je veux en venir.....
Bpon courage, il se peut qu'il y ait des exceptions mais en général on t'en demandera pas +....
Nightmare a écrit:Une interressante :
Pour calculer
On pose :
On obtient :
Interressons nous à
On pose :
Et on obtient :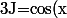e^{x}-\Bigint -sin(x)e^{x}dx)
soit encore :
Finalement :
ainsi :
Et pour finir :modulo constante
:happy3:
bonjour,
L'IPP ne me semble pas la méthode la plus appropriée pour calculer cette intégrale
le mieux est de remarquer que sinx =Im(exp(ix)) (partie imaginaire)
alors I= intégrale(Im(exp(ix))exp(x))= Im(intégrale(exp(x(1+i)))
I= Im(exp(x(1+i)/ (1+i)) ce qui se calcule très rapidement
29 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
