Besoin d'aide sur exercices de mathématiques

[MaurgauxPowa]

Bonjour a toi, le reglement est a lire avant de s'inscrire ...

Je prends des cours par correspondance cet été afin de pouvoir passer en terminale S.
Je suis evalué d'ici pas longtemps afin de voir ma progression.
J'ai reçu des devoirs d'entrainement mais cependant sans corrigé.
J'ai besoin d'aide pour un de ces devoirs que je n'arrive pas à terminer.
Je ne demande pas particulierement les reponses mais disons qu'une demarche detaillée à suivre m'aiderait beaucoup.

Exo 1:

Simplifiez
A= sin(x-(Pie/2)) + 3cos(x+5Pie) - sin(x+(3Pie/2)) - 3cos(x-7Pie)

B= cos((Pie/2)-x) - 2sin((5Pie/2)+x) - cos((5Pie/2)-x) -sin(3Pie+x)



Exo 2:
Soit ABC un triangle équilatéral de coté 3, B' milieu de [AC] et D le point défini par : 4(vecteur)AD=(vecteur)AB+ 3 (vecteur) BC

1) Demontrez que D est barycentre du systeme {(A;3);(B;-2);(C;3)}
Déduisez en que D appartient à la mediatrice du segment [AC]

2)Démontrez que (vecteur)BD= 3/2 (vecteur) BB'

3) Calculez DA^2

4) Déterminez l'ensemble (E) des points M vérifiant la relation :
3MA^2 - 2MB^2 + 3MC^2 = 12
Vérifiez que le centre de gravité G du triangle ABC appartient à (E)


Merci d'avance pour votre aide, toute aide est la bienvenue :we:

[phryte]

Bonjour.
Pour le 1, c'est du cours :
http://www.mathforu.com/cours-53.html

[Jack the ripper]

Exo 2:
Soit ABC un triangle équilatéral de coté 3, B' milieu de [AC] et D le point défini par : 4(vecteur)AD=(vecteur)AB+ 3 (vecteur) BC

1) Demontrez que D est barycentre du systeme {(A;3);(B;-2);(C;3)}
Déduisez en que D appartient à la mediatrice du segment [AC]

2)Démontrez que (vecteur)BD= 3/2 (vecteur) BB'

3) Calculez DA^2

4) Déterminez l'ensemble (E) des points M vérifiant la relation :
3MA^2 - 2MB^2 + 3MC^2 = 12
Vérifiez que le centre de gravité G du triangle ABC appartient à (E)


Salut
L'exercice 2 est plus attrayant :
1) Utilise la définition du barycentre et compare à ton énoncé du début.
Ensuite, pose toi la question de "Qu'est-ce qu'une médiatrice?" et regarde ton barycentre : tu as une similitude entre 2 points. Voici le théorème qui peut t'aider : " Le barycentre de deux points A et B affectés du même coefficient non nul est le milieu de [AB]. On l'appelle l'isobarycentre des points A et B ou encore centre de gravité des points A et B ".
2) Remplace les deux points concernés par B' et n'oublis pas de changer son coefficient, puis applique la définition du barycentre pour un calcul véctoriel.
3) Il faut calculer la longueur du vecteur DA
4)Regarde les coefficients de ton égalité et compare à ton barycentre, développe et tu arriveras à une égalité étant égale à 0, due à la définition de ton barycentre.
" Etant donné trois points A,B,C, il n'existe qu'un point G et un seul tel que :

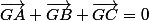
Lorsque A, B et C sont non alignés, ABC est un vrai triangle et le point G est le point d'intersection des médianes : c'est le centre de gravité du triangle".