Besoin d'aide pour les limites

[Anonyme]

J'ai la fonction f(x)=racine(x²+3x+1).
Je dois démonter que y=x+3/2 est asymptote à la courbe représentative C de la fonction f.

Je sais que si :
- lim quand x tend +infini , f(x) - x²-3/2 = 0
- lim quand x tend -infini , f(x) - x²-3/2 = 0

Mais impossible, je tombe toujours sur une forme indéterminée.

Merci d'avance pour votre aide.

[julian]

Bonjour,
Pour démontrer que la droite d'équation y=ax+b est une asymptote oblique à une courbe ,il faut montrer que
ou que
Cordialement.

[Anonyme]

merci mais c'est cela que je n'arrive pas
je tombe toujours sur une forme indéterminée et pas sur 0

[khivapia]

Indice : il faut factoriser par X^2 sous la racine et le sortir (sous forme de valeur absolue de X ! ! ! ! source d'erreur malheureuse, en général les profs n'aiment pas... ), ensuite tu factorise par x ou -x suivant si tu étudies le signe en + ou - l'infini...

Cordialement

[N_comme_Nul]

Salut !

Je te propose de multiplier par la quantité conjuguée :



Le numérateur est égal à -5/4 et le dénominateur tend lorsque

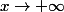
[khivapia]

Oui, ma méthode ne marche pas ici, désolé, mais on retombe sur une forme indéterminée.

A savoir : quand l'une des deux méthodes ne marche pas (entre celle que N_comme_Nul a donnée et celle que j'ai donnée), essayer l'autre, dans 99% des cas elles marchera !

Avec toutes mes excuses pour cette erreur

[julian]

Soi j'ai du mal,soit tu as vraiment fait une faute de frappe,et c'est pourquoi je t'aurai rappelé comment démontrer qu'une courbe admet une asymptote oblique:
tu as écrit
Or ton asymptote a pour équation
Sinon une autre méthode serait d'utiliser la base conjuguée... :marteau:
Edit: message croisé ^^

[Anonyme]

Désolé je me suis trompé :

Je dois donc trouver la lim en - l'infini et + l'infini de :

racine(x²+3x+1) - (x+3/2)

et la ça commence vraiment à me prendre la tête

[Anonyme]

Merci pour ta méthode mais je ne trouve pas -5/4 au numérateur

[bizarre] j'ai du faire une erreur de calcul

[Anonyme]

C'est bon merci