bonjour je voudrais un peu d'aide svp
La question est la suivante :
Résoudre dans R :
Arctan(x)+Arctan(2x)=π/2
Merci!
Arctan(x)+Arctan(2x)=π/2
7 messages
- Page 1 sur 1
Re: Arctan(x)+Arctan(2x)=π/2
Déjà tu peux avoir une idée du nombre de solutions en étudiant les variations de la fonction Arctan(x)+Arctan(2x)
Ensuite tu peux écrire = \frac{\pi}{2} - Arctan(2x)) et trouver une condition nécessaire en prenant la tangente des 2 membres
et trouver une condition nécessaire en prenant la tangente des 2 membres
Ensuite tu peux écrire
Re: Arctan(x)+Arctan(2x)=π/2
Bonjour,
on pourrait aussi écrire+Arctan(2x))=sin(\dfrac{\pi}{2}))
mais le calcul de la parenthèse n'est sans doute pas du niveau lycée
on pourrait aussi écrire
mais le calcul de la parenthèse n'est sans doute pas du niveau lycée
Re: Arctan(x)+Arctan(2x)=π/2
Bonjour,
Calculez la dérivée de+\arctan(2x)=\frac{\pi}{2}) .
.
+\arctan(2x) )'=0) . est de dérivée nulle donc constante sur ]0, +∞[, il reste à calculer pour quelle valeur de x
. est de dérivée nulle donc constante sur ]0, +∞[, il reste à calculer pour quelle valeur de x
+\arctan(2x) )'=\frac{1}{1+x^2}+\frac{2}{1+4x^2}=0) ,
,
Calculez la dérivée de
Re: Arctan(x)+Arctan(2x)=π/2
Bonjour phyelec
quelque chose m'échappe, avec la méthode que tu préconises on ne trouve pas de racine réelle, ou j'ai raté quelque chose?
j'ai trouvé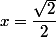
quelque chose m'échappe, avec la méthode que tu préconises on ne trouve pas de racine réelle, ou j'ai raté quelque chose?
j'ai trouvé
Re: Arctan(x)+Arctan(2x)=π/2
Bonjour,
Tu as raison, dans mon calcul j'ai mis un "-", à la place du "+" erreur grossière, sorry so sorry
je suppose que tu as trouvé ce résultat en utilisant+\arctan(1/x) =\frac{\pi}{2}) ,
,
en l'utilisant je trouve le même résultat que toi.
Tu as raison, dans mon calcul j'ai mis un "-", à la place du "+" erreur grossière, sorry so sorry
je suppose que tu as trouvé ce résultat en utilisant
en l'utilisant je trouve le même résultat que toi.
Re: Arctan(x)+Arctan(2x)=π/2
phyelec: j'avais sorti " la grosse artillerie" ,non nécessaire, en utilisant )
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
