Bonjour,
Sur une sphère de rayon R on a un « carré », quatre côtés égaux a et quatre angles égaux alpha.
Calculer son aire A en fonction de R et alpha est facile (formule de Girard) mais comment l'avoir uniquement en fonction de R et a ? Je n'ai pas trouvé de formule alpha=fonction(R,a).
Par curiosité j'ai interrogé quatre IAs (ChatGPT, Perplexity, Deepseek, Le Chat-Mistral) et obtenu quatre réponses toutes différentes, utilisant la formule des cosinus, mais toutes fausses (comme on peut le voir à l'évidence sur des cas particuliers).
Si quelqu'un a une idée pour trouver A=fonction(R,a) merci d'avance.
Aire d'un carré sphérique
5 messages
- Page 1 sur 1
Re: Aire d'un carré sphérique
Salut,
Le triangle formé de deux cotés adjacents du carré et de son centre est isocèle rectangle avec deux angles de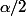 et une hypoténuse de
et une hypoténuse de  . En utilisant la relation duale de la formule des cosinus on en déduit que
. En utilisant la relation duale de la formule des cosinus on en déduit que 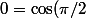=-\cos^2(\alpha/2)+\sin^2(\alpha/2)\cos(a/R))
Le triangle formé de deux cotés adjacents du carré et de son centre est isocèle rectangle avec deux angles de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Aire d'un carré sphérique
Par « son centre » j'imagine que vous voulez dire « une de ses diagonales » , que vous appelez hypoténuse?
Si c'est bien le cas je ne vois pas comment cette diagonale peut être de la même longueur a que les côtés du carré sphérique.
Curieusement, lorsque j'interroge des IAs ou la même IA à des moments différents, parmi les réponses fausses il en est effet une qui fait cette hypothèse erronée.
Par ailleurs, dans cette construction, aucun angle n'est égal à pi/2 (sauf cas très particulier).
Si c'est bien le cas je ne vois pas comment cette diagonale peut être de la même longueur a que les côtés du carré sphérique.
Curieusement, lorsque j'interroge des IAs ou la même IA à des moments différents, parmi les réponses fausses il en est effet une qui fait cette hypothèse erronée.
Par ailleurs, dans cette construction, aucun angle n'est égal à pi/2 (sauf cas très particulier).
Re: Aire d'un carré sphérique
Ma langue à fourchée : ce que je voulais écrire n'est pas "deux cotés adjacents du carré et le centre" mais "deux sommets adjacents et le centre" où le "centre" désigne (entre autre) le point d'intersection des diagonales du carré et l’hypoténuse désigne le coté opposé à l'angle droit du triangle c'est à dire le coté du carré joignant les sommets adjacents choisis.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Aire d'un carré sphérique
D'accord, merci. Entre-temps j'avais finalement trouvé la formule, mais en considérant le triangle isocèle formé par un demi carré et c'est un peu plus compliqué.
Notez quand même qu'avec votre approche il faut prouver que les diagonales se coupent à angle droit, ce qui n'est pas tout-à-fait évident en géométrie sphérique.
Notez quand même qu'avec votre approche il faut prouver que les diagonales se coupent à angle droit, ce qui n'est pas tout-à-fait évident en géométrie sphérique.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
