Bonjour,
Je rentre en maths complémentaires et je bloque déjà ....
Énoncé : https://www.noelshack.com/2020-36-5-159 ... 213904.jpg
Pour la partie 1 je sais que le bocal débordera avec 200 000 lucioles j ai u(n)=10×2^n donc 200 000=10×^n mais je bloque (connais pas les logarithme...)
Partie 2 je bloque totalement
Aide
8 messages
- Page 1 sur 1
Re: Aide
Bonjour,
J'ai hélas bien peu de temps pour vous aider.
Déjà
200 000 = 10*2^n
est équivalent à
20 000=2^n
faute de connaitre les logarithmes (ce qui serait préférable) on sait que la suite (2^n) est strictement croissante
vous pouvez calculer 2^10 puis 2^20
vous constatez que 2^10 < 20 000 < 2^20
et de là...on essaie 2^15...puis...
(il faut trouver le plus petit n tel que 2^n > 20 000)
Proposez une solution et j’essaierai de trouver un peu de temps pour la suite
J'ai hélas bien peu de temps pour vous aider.
Déjà
200 000 = 10*2^n
est équivalent à
20 000=2^n
faute de connaitre les logarithmes (ce qui serait préférable) on sait que la suite (2^n) est strictement croissante
vous pouvez calculer 2^10 puis 2^20
vous constatez que 2^10 < 20 000 < 2^20
et de là...on essaie 2^15...puis...
(il faut trouver le plus petit n tel que 2^n > 20 000)
Proposez une solution et j’essaierai de trouver un peu de temps pour la suite
Re: Aide
Bonjour,
Partie 2)
1)
x(n+1)/x(n) = r.(1-x(n))
x(n+1) = r.(1-x(n))*x(n)
avec fx(n+1) = f(x(n)) ---> f(x) = r.x.(1-x)
2)
a)
r = 0,8 --> x(n+1) = 0,8.(1-x(n))*x(n)
avec x0 = 0,4
x1 = 0,8 * (1-0,4) * 0,4 = 0,192
x2 = 0,8 * (1-0,192) * 0,192 = 0,1241
x3 = 0,8 * (1-0,1241) * 0,1241 = 0,08696
x4 = 0,8 * (1-0,08696) * 0,08696 = 0,06352
... à reporter sur un graphique.
b)
On conjecture que la population de lucioles diminue avec le temps ... et va donc finir par disparaître
c)
x4 = 0,06352 (> 0,05, donc à 5 %)
x5 = 0,8 * (1-0,06352) * 0,06352 = 0,0476 (< 0,05, donc à 5%)
La 5ème année est donc l'année d'extinction.
*****************
Recopier sans comprendre est évidemment inutile.

Partie 2)
1)
x(n+1)/x(n) = r.(1-x(n))
x(n+1) = r.(1-x(n))*x(n)
avec fx(n+1) = f(x(n)) ---> f(x) = r.x.(1-x)
2)
a)
r = 0,8 --> x(n+1) = 0,8.(1-x(n))*x(n)
avec x0 = 0,4
x1 = 0,8 * (1-0,4) * 0,4 = 0,192
x2 = 0,8 * (1-0,192) * 0,192 = 0,1241
x3 = 0,8 * (1-0,1241) * 0,1241 = 0,08696
x4 = 0,8 * (1-0,08696) * 0,08696 = 0,06352
... à reporter sur un graphique.
b)
On conjecture que la population de lucioles diminue avec le temps ... et va donc finir par disparaître
c)
x4 = 0,06352 (> 0,05, donc à 5 %)
x5 = 0,8 * (1-0,06352) * 0,06352 = 0,0476 (< 0,05, donc à 5%)
La 5ème année est donc l'année d'extinction.
*****************
Recopier sans comprendre est évidemment inutile.
Re: Aide
Bonjour.
Plutôt que de lancer les solutions (de façon totalement illisibles d'ailleurs, car mal mises en page), il serait préférable de faire réfléchir le questionneur.
En tant qu'enseignant (sur Bordeaux en plus, ville du questionneur), je suis abasourdi de voir ça... et ne m'étonne donc plus du niveau de plus en plus décroissant des élèves (dans la mesure où on leur donne tout sur les forums, il n'y a plus à réfléchir).
Donner une réponse toute faite, comme cela est régulièrement fait sur ce forum, revient à bloquer l'apprentissage et ne sert à rien, sinon à flatter l'égo de la personne qui donne la solution.
Quand on est élève en maths complémentaires, comme c'est le cas ici, c'est qu'on a abandonné la spécialité mathématiques et donc que l'on n'est pas nécessairement à l'aise avec les maths. Il faut donc une approche plus méthodique et souple.
La réponse de Rdvn est intéressante car elle montre une méthode pour trouver l'entier .
.
En effet, pour trouver le premier entier pour lequel
pour lequel 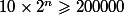 , on peut d'abord diviser par 10 à droite et à gauche du signe, ce qui donne
, on peut d'abord diviser par 10 à droite et à gauche du signe, ce qui donne 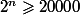 , puis utiliser la calculatrice en construisant un tableau de valeurs de
, puis utiliser la calculatrice en construisant un tableau de valeurs de  (mode "suite" > on entre l'expression
(mode "suite" > on entre l'expression  > puis "Table" par exemple) et on constate que l'on a :
> puis "Table" par exemple) et on constate que l'on a :

La première valeur à retenir est donc n = 15 car c'est la première valeur pour laquelle on dépasse 20000.
Concernant la deuxième partie, ce qui est important pour la question 1 est "en traduisant cette proportionnalité" : il y a proportionnalité entre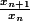 et
et ) , qui se traduit par l'égalité :
, qui se traduit par l'égalité : 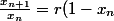) . À vous de poursuivre et d'utiliser cela pour arriver à une égalité de la forme
. À vous de poursuivre et d'utiliser cela pour arriver à une égalité de la forme 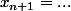 en fonction de
en fonction de  .
.
Pour la question 2, on doit mettre sur l'axe des abscisses (horizontal), puis trouver l'image de ce nombre par la fonction f. On le "projette" verticalement sur la courbe représentative de f afin d'obtenir un point, que l'on va projeter horizontalement sur la droite; ce dernier point obtenu sera ensuite projeté verticalement sur l'axe des abscisses pour obtenir
sur l'axe des abscisses (horizontal), puis trouver l'image de ce nombre par la fonction f. On le "projette" verticalement sur la courbe représentative de f afin d'obtenir un point, que l'on va projeter horizontalement sur la droite; ce dernier point obtenu sera ensuite projeté verticalement sur l'axe des abscisses pour obtenir  . On répète ceci jusqu'à obtenir les 4 premiers termes sur l'axe des abscisses.
. On répète ceci jusqu'à obtenir les 4 premiers termes sur l'axe des abscisses.
La conjecture doit s'appuyer sur l'observation des termes construits : comment se comportent-ils ? La suite semble-t-elle croissante ou décroissante ? Les termes semblent-ils se rapprocher d'un nombre ?
Enfin, pour la question c, on ne doit plus s'appuyer sur le graphique car il faut déterminer l'année (donc le nombre n) tel que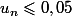 (qui correspond à 5%). On doit donc résoudre cette dernière inéquation comme on a résolu la précédente (avec la calculatrice si on ne connaît pas le logarithme).
(qui correspond à 5%). On doit donc résoudre cette dernière inéquation comme on a résolu la précédente (avec la calculatrice si on ne connaît pas le logarithme).
Voilà ce que j'appelle apporter une véritable aide, le but étant que le questionneur sache répondre aux questions lors des contrôles (où les intervenants de ce forum ne pourront plus leur donner les réponses toutes faites).
Plutôt que de lancer les solutions (de façon totalement illisibles d'ailleurs, car mal mises en page), il serait préférable de faire réfléchir le questionneur.
En tant qu'enseignant (sur Bordeaux en plus, ville du questionneur), je suis abasourdi de voir ça... et ne m'étonne donc plus du niveau de plus en plus décroissant des élèves (dans la mesure où on leur donne tout sur les forums, il n'y a plus à réfléchir).
Donner une réponse toute faite, comme cela est régulièrement fait sur ce forum, revient à bloquer l'apprentissage et ne sert à rien, sinon à flatter l'égo de la personne qui donne la solution.
Quand on est élève en maths complémentaires, comme c'est le cas ici, c'est qu'on a abandonné la spécialité mathématiques et donc que l'on n'est pas nécessairement à l'aise avec les maths. Il faut donc une approche plus méthodique et souple.
La réponse de Rdvn est intéressante car elle montre une méthode pour trouver l'entier
En effet, pour trouver le premier entier
La première valeur à retenir est donc n = 15 car c'est la première valeur pour laquelle on dépasse 20000.
Concernant la deuxième partie, ce qui est important pour la question 1 est "en traduisant cette proportionnalité" : il y a proportionnalité entre
Pour la question 2, on doit mettre
La conjecture doit s'appuyer sur l'observation des termes construits : comment se comportent-ils ? La suite semble-t-elle croissante ou décroissante ? Les termes semblent-ils se rapprocher d'un nombre ?
Enfin, pour la question c, on ne doit plus s'appuyer sur le graphique car il faut déterminer l'année (donc le nombre n) tel que
Voilà ce que j'appelle apporter une véritable aide, le but étant que le questionneur sache répondre aux questions lors des contrôles (où les intervenants de ce forum ne pourront plus leur donner les réponses toutes faites).
Cours particuliers par webcam : https://cours-maths-webcam.fr/
LaTeX, Maths & Python : https://www.mathweb.fr/
LaTeX, Maths & Python : https://www.mathweb.fr/
Re: Aide
+1
Ce n’est malheureusement pas le seul forum dans ce cas .Le plus atterrant est certainement nosdevoirs.fr où il y a une course stupide et futile au meilleur classement dans lequel participent également les modérateurs , la véritable aide pour les élèves n’étant pas la priorité !
Je me permets de donner une citation dont la paternité est incertaine :
-tu me dis , j’oublie
-tu m’enseigne, je me souviens
-tu m’implique, j’apprends
Ce n’est malheureusement pas le seul forum dans ce cas .Le plus atterrant est certainement nosdevoirs.fr où il y a une course stupide et futile au meilleur classement dans lequel participent également les modérateurs , la véritable aide pour les élèves n’étant pas la priorité !
Je me permets de donner une citation dont la paternité est incertaine :
-tu me dis , j’oublie
-tu m’enseigne, je me souviens
-tu m’implique, j’apprends
Re: Aide
A messieurs les donneurs de leçon, (evaristeG et JeanP)
Et bien moi je me moque de vos opinions ...
Les suivre fait qu'on en est arrivé là où on est, soit dans le médiocrité.
Il n'est pas question de tout expliquer jusque la moindre virgule.... on n'est pas dans une salle de cours où on se tait en buvant les paroles de ceux qui ont (ou pensent avoir) le savoir.
C'est à l'étudiant de se creuser pour essayer de comprendre comment relier son énoncé à la réponse "sibylline" qu'il reçoit et ainsi en comprendre le pourquoi. C'est ainsi qu'il progressera ...
Ce n'est certainement pas en décortiquant les problèmes en 10 sous questions (comme on le fait actuellement) et en expliquant la marche à suivre à chaque carrefour qu'on améliorera le raisonnement global (réduit à quasi rien actuellement)
Gardez donc votre méthode ... que vous pensez bonne.
Les étudiants continueront à suivre les indications du GPS à chaque carrefour ... et ne développeront jamais leur sens de l'orientation.
Peut-être devriez-vous vous demander pourquoi la plupart des étudiants en dernière année secondaire serait le genou en terre devant des examens de seconde d'il y a quelques années.
Il y a diverses raisons évidemment dont une que vous sembler réfuter.
Alors de grâce, laissez les autres répondre comme ils l'entendent.

Et bien moi je me moque de vos opinions ...
Les suivre fait qu'on en est arrivé là où on est, soit dans le médiocrité.
Il n'est pas question de tout expliquer jusque la moindre virgule.... on n'est pas dans une salle de cours où on se tait en buvant les paroles de ceux qui ont (ou pensent avoir) le savoir.
C'est à l'étudiant de se creuser pour essayer de comprendre comment relier son énoncé à la réponse "sibylline" qu'il reçoit et ainsi en comprendre le pourquoi. C'est ainsi qu'il progressera ...
Ce n'est certainement pas en décortiquant les problèmes en 10 sous questions (comme on le fait actuellement) et en expliquant la marche à suivre à chaque carrefour qu'on améliorera le raisonnement global (réduit à quasi rien actuellement)
Gardez donc votre méthode ... que vous pensez bonne.
Les étudiants continueront à suivre les indications du GPS à chaque carrefour ... et ne développeront jamais leur sens de l'orientation.
Peut-être devriez-vous vous demander pourquoi la plupart des étudiants en dernière année secondaire serait le genou en terre devant des examens de seconde d'il y a quelques années.
Il y a diverses raisons évidemment dont une que vous sembler réfuter.
Alors de grâce, laissez les autres répondre comme ils l'entendent.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
