Aide svp 2 questions

[zerow2001]

Salut, j'ai besoin de l'aide svp
j'ai jamais vu ce genre d'exercice

Salut !

1)Df = IR-{-1 ; 1}
2)( ∀x∈Df-{ 0 } ) :

LA QUESTION 1 : Conclure la relation entre

LA QUESTION 2: Montrez que si a est le racine de l'équation alors 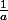est le racine de l'équation
Merci d'avance

[Carpate]

j'ai jamais vu ce genre d'exercice :

Si tu te contentes de faire toujours des exercices que tu as déjà vus, ça ne t'aidera pas beaucoup à progresser
1) remplacer tout bêtement x par 1/x et effectuer le produit f(x) . f(1/x)
2) appliquer la formule de la dérivée d'un produit pour dériver : f(x).f(1/x) = 1
Il n'y a aucune astuce

[zerow2001]

C'est pas ca, j'ai deja fait le premier exercice de f(x) *f(1/x)
j'ai besoin d'aide avec les question en gras
et merci en tous cas

[zerow2001]

+ j'ai deja fait l'exerice du dérivé aussi, j'ai besoin d'aide seulement avec le dernier exercice

[Carpate]

On dérive les 2 termes de la relation

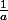
Montrez que si a est le racine de l'équation f'(x)=0 alors est racine de l'équation

Ce n'est pas plutôt : montrez que si a est le racine de l'équation f'(x)=0 alors a est racine de l'équation
Car pour !

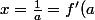[zerow2001]

Hahahhaha, désolé

[Carpate]

Suite :
Donc
Comme ne s'annule pas sur , il vient
Je n'arrive pas à comprendre où l'auteur de l'énoncé veut en venir . Y a-t-il d'autres questions avant et après celles que tu a écrites ?
Est-ce que tu pourrais écrire mot pour mot l'énoncé complet ?

[zerow2001]

Oui biensur !

La suite de l'énoncé :

3) Montrez que
(J'ai deja fait cette question)

4) Verifie que : x^{4}-2x^{3}-2x^{2}-2x+1=x^{2}[(x+\frac{1}{x})^{2}-2(x+\frac{1}{x})-4] (J'ai deja fait cette question)

5) Etudie la signe de f'(x) et tracer le tableau de variations de f

PARTIE II :

Soit h une foction définie avec :


1) Montrez que h est continue à gauche de 1 et à gauche de -1 (J'ai deja fait cette question)
2) Montrez que : (PAS ENCORE FAIT)
3) Calculer : Que conclues-tu ? (PAS ENCORE FAIT)
4) Est-ce que f est dérivable à gauche de -1 ?
5) Etudie les sections infinie de h dans +oo et -oo ((J'ai deja fait cette question))
6) Tracez la courbe((J'ai deja fait cette question))

[Carpate]

C'est une astuce pour faire apparaître qui se simplifie en
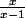
J'arrête pour ce soir, d'autres prendront sans doute la suite ...

[zerow2001]

C'est pas grave, quelle suite ?

[Carpate]

Ca m'intrigue ; comment as-tu montré que h est continue à droite de -1 et à gauche de 1 si h(1) = h(-1) = 0 ?