QuestionS Maths 1S (l'aide la plus rapide sera la bienvenue, mais complete svp aussi)

[Divayth]

Salut a tous,

J´aurai quelques questions a vous posé et auquels je n´arrive pas a repondre, alors si vous avez un peu de temps a me consacré, je vous serai infiniment reconnaissant d´eclairer ma lanterne :

- en trigonométrie, je n´arrive pas a effectuer le passage des coordonnées cartésiennes aux coordonnées polaires...
La formule avec A(x;y) par exemple. Pour calculer le rayon je fais R=OA=V(x²+y²). Ensuite pour calculer x (deja je vois pas tres bien ce que c´est...) avec x=R*cosO (le cos non plus je vois pas trop ce que c´est. Avec y c´est pareil...

- dans les fonctions, comment par exemple on démontre avec des absices chercher l´equation : x^3 - 4x² + 2x + 3 = 0
C´est quoi démontrer 3 réels avec sa ?
En fait je ne comprends pas comment, avec une equation pareille, on arrive a trouvé des points d´abscisse...
Aussi, quand l´equation est sous cette forme, je n´arrive pas a la factorisée, je ne comprend pas comment faire ... xD

- Dans le barycentre maintenant, comment on prouve que des droites sont concourrantes en 1 points ?
Comment déterminer l´ensemble E des points M du plan tel que ||MA + 4MB - 3MC|| = ||MA + MB||

Ce que je donne ici ne sont que des exemples, par conséquent, le resultat ne m´interesse pas. Je voudrais comprendre par moi meme, afin de combler mes lacunes dans les mathématiques.

Je sais que j´ai beaucoup ecrit mais les explications elles ne me paraissent pas difficiles et rapide a ecrire si on les a comprises, c´est pourquoi je vous demande un peu de votre temps.

Par exemple, pour les barycentres, me dire qu´il faut au début quon ai sous la forme blablabla, on utilise la formule nanana pour arriver au resultat tout la FORME blablanana et apres je rechercherai par moi meme;seulement la je bloque...

Encore une fois, merci infiniment a celui ou celle qui m´aidera !

[fonfon]

salut,

- en trigonométrie, je n´arrive pas a effectuer le passage des coordonnées cartésiennes aux coordonnées polaires...
La formule avec A(x;y) par exemple. Pour calculer le rayon je fais R=OA=V(x²+y²). Ensuite pour calculer x (deja je vois pas tres bien ce que c´est...) avec x=R*cosO (le cos non plus je vois pas trop ce que c´est. Avec y c´est pareil...

x et y ce sont les coordonnées cartesienne
sinon un rappel de cours

si un point M a pour coordonnées (x;y) dans le repère orthonormal direct et pour coordonnées polaires dans le repere polaire
alors on a:

et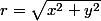

moi je te conseille de revoir ton cours

je te donne un exemple:

par ex:
le plan est rapporté à un repére orthonormal direct

on considere donner ses coordonnées polaires dans

on a :
donc r=2

or on sait que:
et

donc on remplace on sait que x=1 et que y=V3 et on vient de calculer r=2 soit:

et

donc
et

donc en utilisant le cercle trigo ou les valeurs remarquables on trouve que:

[Divayth]

Merci ! Grace a ton exemple j'ai parfaitement compris.
En fait, il y a une erreur dans mon livre, pour sa que je trouvais des trucs incosidérés xD

PS : un ami m'as aussi expliquer les fonctions, meme si ce n'est pas totalement claire, la seule chose qui me reste a faire est d'y potasser un peu seul.

Plus que les barycentres, mais je vais essayé de me débrouiller ... mais un peu d'aide serait la bienvenue, alors n'hesitez pas ! :p

[Calo]

On fait ça en 1e S !!

Ah c'est horrible, on est en retard dans le programme alors !! :-:

[fonfon]

Re,

- dans les fonctions, comment par exemple on démontre avec des absices chercher l´equation : x^3 - 4x² + 2x + 3 = 0
C´est quoi démontrer 3 réels avec sa ?
En fait je ne comprends pas comment, avec une equation pareille, on arrive a trouvé des points d´abscisse...
Aussi, quand l´equation est sous cette forme, je n´arrive pas a la factorisée, je ne comprend pas comment faire ... xD

je comprends pas de trop ce que tu veux au debut c'est pas tres clair

par contre

Aussi, quand l´equation est sous cette forme, je n´arrive pas a la factorisée, je ne comprend pas comment faire

en 1ere quand tu as une equation de ce type
il faut que tu cherches une racine evidente parmi -3,-2,-1,0,1,2,3

ici je te la donne directe je ne fais pas tout les tests on remarque que 3 est racine evidente car:


donc est factorisable par

donc s'ecrit avec q(x) un polynôme du second degré donc q(x) est de la forme ax²+b+c

donc on a:



pour trouver les coefficients a,b et c on va proceder par identification

on developpe

or x^3-4x^2+2x+3=ax^3+x^2(b-3a)+x(c-3b)-3c

or deux polynôme sont egaux ssi ils ont le même defré avec les coefficients des termes de même degré egaux

donc ici on obtient un systeme:




donc


il ne reste plus qu'à chercher les racines du polynôme x²-x-1 et tu auras la forme factoriser complete

mais generalement tu es guidé dans un exercice en 1ere

A+

[Divayth]

Un grand merci a toi ! Tu me sauves !

Calo : tu ne fais peut etre pas les chapitres dans le meme ordre que nous, ne t'inquiete pas ;)

[fonfon]

Salut,

- Dans le barycentre maintenant, comment on prouve que des droites sont concourrantes en 1 points ?
Comment déterminer l´ensemble E des points M du plan tel que ||MA + 4MB - 3MC|| = ||MA + MB||

pour prouver que des droites sont concourantes en un point il faut montrer que ce même point appartient à toutes les droites

ex:

soit ADCD un quadrilatere , I milieu de [AC] et J milieu de [BD].Souit K le point tel que ,L le point tel que et M milieu de [LK]
1) justifier l'existence du barycentre G du systeme : [ ( A,1),(B,2),(C,1),(D,2)]
en regroupant les point de différntes facons montrer que G appartient aux deux droites (KL) et (IJ)

1)le bary du système [ ( A,1),(B,2),(C,1),(D,2)]
existe, car la somme des coefficients du système est non nul.

ensuite on va montrer que G appartient à (KL)

tu sais que donc K est bary de [ ( A,1),(B,2)]

de mêm on a :
donc L est bary de [(C,1);(D,2)]

or G est bary [(A,1),(B,2),(C,1),(D,2)] donc par assciativité G est bary [(K,1+2),(L(1+2)])=[(K,3),(L,3)]

donc G appartient à (KL)

on fait la même chose pour montrer que G appartient à(IJ)

I milieu de [AC] donc I bary de [(A,1),(C,1)]
J milieu de [BD] donc J bary de [(B,1),(D,1)] ( on ne change pas le baycentre en multipliant (ou en divisant) les coefficients pas un même réel non-nul) donc J est bary de [(B,2),D,2)]

or G est bary [(A,1),(B,1),(C,1),(D,2)]=[(A,1),(C,1),(B,2),(D,2)] donc par associativité G est bary de [(I,2),(J,4)] donc G appartient à (IJ)

donc G appartient à (KL) et (IJ)....

Comment déterminer l´ensemble E des points M du plan tel que ||MA + 4MB - 3MC|| = ||MA + MB||

je n'ecrit pas les vecteurs (c'est un peu long)
ici l'idée est qu'il faut faire intervenir des barycentres

soit G1 bary de [(A,1),(B,4),(C,-3)] (coefficient que l'on retrouve dans ||MA+4MB-3MC||
et G2 bary de [(A,1),(B,1)] (coefficient quel'on retrouve dans ||MA+MB||)

donc on introduite G1 soit
||MG1+G1A+4MG1+4G1B-3MG1-3G1C||=||MG1+4MG1-3MG1+G1A+4G1B-3G1C|| or G1 bary de [(A,1),(B,4),(C,-3)] donc G1A+4G1B-3G1C=0

donc ||MA+4MB-3MC||=||MG1+4MG1-3MG1|| donc ||MA+4MB-3MC||=||2MG1||

on fait pareil avec G2
||MA+MB||=||MG2+G2A+MG2+G2B||
||MA+MB||=||MG2+MG2+G2A+G2B||

or G2 bary de [(A,1),(B,1)] donc G2A+G2B=0

donc
||MA+MB||=||2MG2||

donc

||MA + 4MB - 3MC|| = ||MA + MB||

||2MG1||=||2MG2||

MG1=MG2

donc M est équidistant à G1 et G2 et appartient donc à la médiatrice de [G1G2] (ensemble des points)

Ps: l'ensemble des points M change suivant ce que l'on te propose comme exercice

A+
(j'espere ne pas avoir fais d'erreur en tapant car c'etait un peu long)