Aide pour exercice

[jakmartin]

bonjour j'ai un probléme avec un exercice je ne le comprend pas et je n'y arrive pas du tout merci pour votre aide.
soit f la fonction définie sur ]1;+l'infini[ par f(x)=ln(x^3-x^2)
1.justifier que pour tout x de l'intervalle ]1;+l'infini[ f(x) est défini
2.déterminer lim f(x) quand x tend vers 1 et quand x tend vers +l'infini
3.on note f' la fonction dérivé de f, vérifier que pour tout x dans l'intervlle ]1;+l'infini[, f'(x)=(3x-2)/(x(x-1))
dresser le tableau de variation de la fonction f sur l'intervalle ]1;+l'infini[
4.a. j'ai réussi il fallait monter que f(x)=0 admet une solution c'était avec le TVI
b. démonter que f(x) est strictement positif sur ]alpha;+l'infini[
5. soit h la fonction définie sur ]1;+l'infini[ par: h(x)=2x ln(x)+(x-1) ln(x-1)
pour tout x de ]1;+l'infini[ calculer h'(x)
en déduire une primitive de la fonction f sur ]1;+l'infini[

[Dinozzo13]

Salut !
Alors pour commencer :
1. Démontre le domaine de définition de en sachant que la fonction 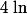est toujours strictement positive.
2. Détermine ; pour l'autre, détermine d'abord , tu en déduis alors
3. Ici dis sur quel intervalle est-elle dérivable puis calcule-la. Pour étudier les variations de résous .