Aide pour un exercice :p

[Benco]

Boujour j'aimerais de l'aide pou le b) de la question 2), merc d'avance :p

[Imod]

Tu peux remarquer que les deux points d'intersections M(x,f(x)) et M'(x',f(x')) ont mêmes ordonnées et 2xx'=3 ou encore x'=3/(2x) . I a donc pour coordonnées I((x+x')/2,f(x)) il te reste à calculer et à montrer que c'est égal à (x+x')/2 .

Imod

[Benco]

Merci de votre aide mais je n'arrive pas à voir comment est ce que vous trouvez 2xx'=3 ou bien x'=3/(2x)
Merci d'avance pour votre explication :)

[Imod]

J'ai résolu l'équation f(x)=f(x') . Essaie de le faire seul , si tu n'y arrive pas je te donnerais des indices .

Imod

[Benco]

j'ai essayé et je trouve x'(2x²racine3 + 3racine3) = x(2x'²racine3 + 3racine3)
je ne suis pas sur de mon resultat et s'il est bon je bloque à cet endroit.

[Imod]

f(x)=f(x') se traduit par :



...

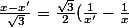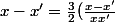Je te laisse finir .

Imod

[Benco]

Merci pour votre Imod, j'obtiens le même résultat que ce que vous m'avez indiqué ;)