Addition d'exponentielles

[Aktar]

Bonjour,

Est-ce qu'il y a une façon simple d'écrire sous forme exponentielle la somme de deux exponentielles?

C'est à dire de trouver sous forme exponentielle le résultat du calcul ?

Merci beaucoup!

[aviateur]

Bjr
De façon générale la réponse est non. Maintenant cette expression dans un calcul peut être transformée pour le besoins de la cause.
Comme par exemple si a= ix et b=-ix alors cela se simplifie et donne 2 cos(x)

[Aktar]

Merci,
En fait mon problème est le suivant:

J'ai deux fonctions logistiques avec chacune deux paramètres. Je cherche la troisième forme logistique qui va me permettre de remplir la condition , avec



et



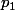
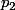
Je sais donc que et sont compris entre 0 et 1 avec

Les paramètres et sont estimés de tel sorte que

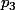
Je peux donc facilement calculer car je connais les coefficients et .

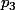
Mon soucis c'est que je ne veux pas car je peux l'obtenir facilement... mon objectif est de retrouver .

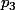
Mon idée était donc de retrouver la forme logistique de avec

et ensuite simplement inverser le signe de la somme car

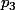
Je pourrais facilement l'obtenir en résolvant l'équation logistique de , mais en realité c'est plus compliqué car les paramètres sont variants dans le temps et dépendent d'une variable et d'un autre coefficient qui n’apparaissent pas ici.

Donc pour facilité les choses, je me demandais s'il n'y avait pas possibilité d'obtenir sous une forme logistique le résultat du calcul ,

ce qui reviendrait à additionner simplement et à mettre le résultat sous forme exponentielle.

Merci!

[Black Jack]

C'est quoi ?

[aymanemaysae]

Bonjour ;

En posant alors tu as ;

ensuite tu as : ;

;

et enfin tu as : ;