Bonjour, j'aurai besoin d'aide sur la fin d'un exercice.Voici l'énoncé:
Dans le plan affine,ABC triangle rectangle en A, I milieu de [AB] et J centre de gravité de ABC. Pour tout reel m, different de -1/3, Gm le barycentre de (A;1),(B;m),(C;2m). Pour tout point M du plan, on note vecteur VM=3vecteur MA-vecteur MB -2vecteur MC.
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant.J'ai reussi les 3 premieres mais je bloque sur celle-ci:
-Pour tout m, distinct de -1/3, vecteur AGm est colinéaire à vecteur AG-1
-IBG-1/2 est un triangle rectangle.
- Pour tout point P de (AG-1), il existe un reel m tel que P=Gm.
Merci pour tout aide !!
1ereS:exercice de géométrie
7 messages
- Page 1 sur 1
salut,
1)
si m#-1/3, la somme des coefficients 1+m+2m n'est pas nulle donc existe er :
existe er :
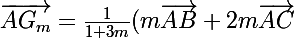=\frac{m}{1+3m}(\vec{AB}+2\vec{AC}))
en particulier on a:
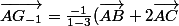=\frac{1}{2}(\vec{AB}+2\vec{AC}))
ce qui donne en remplaçant dans l'expression de

donc les vecteurs et
et  sont colinéaires
sont colinéaires
tu n'arrives vraiment pas les 2 dernières?
Bonjour, j'aurai besoin d'aide sur la fin d'un exercice.Voici l'énoncé:
Dans le plan affine,ABC triangle rectangle en A, I milieu de [AB] et J centre de gravité de ABC. Pour tout reel m, different de -1/3, Gm le barycentre de (A;1),(B;m),(C;2m). Pour tout point M du plan, on note vecteur VM=3vecteur MA-vecteur MB -2vecteur MC.
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant.J'ai reussi les 3 premieres mais je bloque sur celle-ci:
-Pour tout m, distinct de -1/3, vecteur AGm est colinéaire à vecteur AG-1
-IBG-1/2 est un triangle rectangle.
- Pour tout point P de (AG-1), il existe un reel m tel que P=Gm.
1)
si m#-1/3, la somme des coefficients 1+m+2m n'est pas nulle donc
en particulier on a:
ce qui donne en remplaçant dans l'expression de
donc les vecteurs
tu n'arrives vraiment pas les 2 dernières?
-IBG-1/2 est un triangle rectangle.
par defintion on a:
{(A;1);(B;-1/2);(C,-1)}
on en deduit que:
la droit
Comme I est le milie de [AB], la droite
- Pour tout point P de (AG-1), il existe un reel m tel que P=Gm.
pour tout point P de
d'apres la question 4.
donc
maintenant essaie de conclure suivant que
lorsque gamma=2/3 on a 0=-2/3
losque gamma different de 2/3, je ne vois pas comment conclure.
est ce que m doit etre different de -1/3 ?
c'est pas gamma c'est lamda
si
si
conclusion:
Le point P de
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
