Problème de parabole
9 messages
- Page 1 sur 1
Problème de parabole
Bonjour. Je crée un jeu vidéo. Et j'ai besoin d'une equation de parabole pour faire bouger un sprite-objet. J'ai le point de départ et le point d'arivée. La parabole peut être toujours de même A. Je pete les plombs. Pouvez-vous m'aider ?
Re: Problème de parabole
bonjour,
soient trois points,B(x_2;y_2);C(x_3;y_3)) dans le plan rapporté à un repère affine.
dans le plan rapporté à un repère affine.
Le quotient(x-x_3)}{(x_1-x_2)(x_1-x_3)}) s'annule pour
s'annule pour 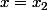 et
et 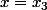
et vaut en
en 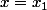
Le quotient(x-x_3)}{(x_1-x_2)(x_1-x_3)}y_1) s'annule pour
s'annule pour 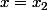 et
et 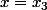
et vaut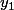 en
en 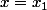
on en déduit que l'expression (polynôme de la variable x):
(x-x_3)}{(x_1-x_2)(x_1-x_3)}y_1+\dfrac{(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}y_2+\dfrac{(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)}y_3)
est un trinôme du second degré (polynôme de degré 2) dont la courbe représentative contient les points A,B et C
soient trois points
Le quotient
et vaut
Le quotient
et vaut
on en déduit que l'expression (polynôme de la variable x):
est un trinôme du second degré (polynôme de degré 2) dont la courbe représentative contient les points A,B et C
Re: Problème de parabole
Merci... Je comprend un peu... Mais si je cherche une formule y=ax2 +bx +c quel rapport avec votre plynome ? Help.
Re: Problème de parabole
Merci. Je l'ai fait ça donne une formule longue et com0liquée mais ça devrait marcher...
Re: Problème de parabole
Cryptadone a écrit:Merci... Je comprend un peu... Mais si je cherche une formule y=ax2 +bx +c quel rapport avec votre polynome ? Help.
Les deux méthodes devraient donner le même polynôme. je me lance dans les calculs de vérification
de l'égalité des deux polynômes.
Après calculs, les deux polynômes sont les mêmes.
Pour a, je trouve
Pour c, je trouve
Pour b, je trouve
Re: Problème de parabole
en utilisant les déterminants et en réarrangeant, je trouve la même chose que mathelot
Re: Problème de parabole
Merci beaucoup. Ça marche ( je crée un jeu de basket- tout simple) la parabole c'est pour le shoot du joueur et le rebond sur le panier si le tir est raté.. En python. Language génial...
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
