Non LB2 je n'ai pas trouvé de facon plus elegante de résoudre ce probleme que ce qu'on nous a appris
dans le MOOC du MIT courses.
edx.org/courses/course-v1:MITx+6.431x+3T2018/courseware/Unit_10_Markov_chains .
a savoir mettre les equations des absorbing state a zero, les aborbing states sont tous ceux sur les bords
(quand le robot tombe) et resoudre le systeme d'equations
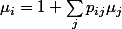
avec SageMath . a la main c'est un travail de benedictain !
j'ai mis la matrice de transfert dans la derniere cellule. je trouve la meme valeur que BEN,
pour ma matrice le centre de la table est
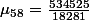
quand vous executez le code Sagemath que j'ai deposé sur cocalc.com il faut cliquer sur "fetch additional output" en bas de la cellule, sinon le code ne s'execute pas entierement.
code Gambler ruin 2D sur cocalc.comdans le post j'ai voulu y faire figurer le système d'equation en Latex mais ca ne fonctionne pas.

ci dessous c'est la matrice de la representation topologique de la chaine de Markov.
je n'ai pas mis la matrice de transfert (trop grande), elle figure dans le code (executer le code de la 3em cellule pour obtenir le Latex).
mon code fonctionne aussi pour une table rectangulaire (mettre des valeurs différentes a rstateNumber et cstateNumber (correspondent au deux cotés de la table), et aussi si les 4 déplacements ne sont pas equiprobable, il suffit de modifier les valeurs:
# row cell number
rstateNumber = 11
#column cell number
cstateNumber = 11
#########################
#changer les valeurs des probas de deplacement si vous le souhaitez
# bien sur il faut que la somme fasse 1

p_right=1/4
p_up=1/4
p_left=1/4
p_down=1/4
PS: @LB2 les tentatives de "simplifications" dans le post dont tu donnes le lien, ne m'ont pas convaincue
la seul difficulté dans ce probleme (et ca ne l'est pas beaucoup est de remplir correctement la matrice de transition)
et le probleme se limite a une simple résolution d'un systeme d'equations, quand on utilise la theorie des chaines de Markov.
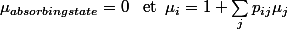
)

si j'avais su j'aurais pas venu.
 .)
.) . je ne sais pas d'ailleurs si cette methode etait connue.
. je ne sais pas d'ailleurs si cette methode etait connue.

