Bonjour et merci pour ton attention à ce problème, tes recherches me font plaisir
 Notation
Notation 
le nombre de distributions correctes de boules sans tenir compte de l'ordre des couleurs

le nombre de distributions correctes de boules en tenant compte de l'ordre des couleurs
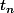
le nombre total de distributions
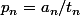
la probabilité recherchée
Exemple le cas

et
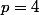
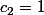
car on ne peut avoir que ABAB
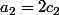
car on peut mettre à la première place A ou B ce qui donne ABAB ou BABA
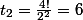
car on ordonne les 4 boules mais pour chaque paire, il faut diviser par 2 car peu importe qui est la première boule ou la dernière boule ce qui donne AABB, ABAB, ABBA, BABA, BAAB, BBAA
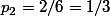
bravo tu as raison
 Exemple
Exemple le cas
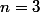
et
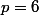
sans tout détailler cette fois
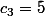
car on ne peut avoir que ABACBC, ABCABC, ABCACB, ABCBAC, ABCBCA
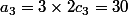
car on peut mettre à la première place A ou B ou C et ensuite (B ou C) ou (A ou C) ou (A ou B)
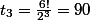
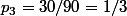
tu n'étais pas très loin, tu as surement compté un cas en trop dans
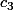
De manière plus générale on va trouver
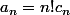
car

correspond au nombre de façon d'ordonner les

couleurs
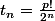
donc ton dénominateur est correct

!}=\frac{c_n (2n)(2n-2)(2n-4)...4\times 2}{(2n)(2n-1)(2n-2)(2n-3)(2n-4)...4\times 3\times 2}=\frac{c_n}{(2n-1)(2n-3)...3})
Bon mais maintenant que vaut

? C'est un problème difficile, on va essayer de le faire par récurrence
Une configuration comptabilisée dans

est de la forme A.....A...., une boule A est à la première place et on se demande où mettre la seconde boule A connaissant tous les

précédents
- A partir d'une configuration comptabilisée dans
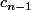
on peut rajouter A entre n'importe quelles boules ou après (pas avant car il y a déjà A), ce qui donne
=2n-2)
places.
Attention ce n'est pas suffisant car en faisant cela notre seconde boule A ne sera jamais entourée par 2 boules de la même couleur puisque cette configuration n'existe pas dans
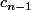
- A partir d'une configuration comptabilisée dans
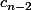
on peut rajouter BAB entre n'importe quelles boules ou après ou avant, ce qui donne
+1=2n-3)
places
Attention ce n'est pas suffisant car en faisant cela notre BAB ne sera jamais entouré par 2 boules de la même couleur puisqu cette configuration n'existe pas dans
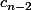
- A partir d'une configuration comptabilisée dans
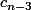
on peut rajouter CBABC entre n'importe quelles boules ou après ou avant, ce qui donne
+1=2n-5)
places
...
Au final
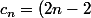c_{n-1}+(2n-3)c_{n-2}+(2n-5)c_{n-3}+(2n-7)c_{n-4}+...+5c_2+3c_1+c_0)
avec
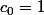
et
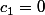
Je te passe le détail des calculs, c'est difficilement accessible au niveau lycée et je comptais un peu sur les lecteurs pour trouver mieux mais on trouve
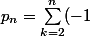^k \frac{C_{2n-k}^k}{(2n-1)(2n-3)(2n-5)...(2n-2k+1)})
Cette suite

est croissante, c'est logique, plus on a de couleurs, plus on a de chances de ne pas tomber sur la même couleur à la suite. Par contre ce qui est amusant c'est qu'elle converge vers
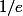
autrement dit elle n'augmente pas beaucoup puisqu'elle part de
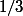
pour

 ou plus difficiles
ou plus difficiles 

