Test pour les IMO
Olympiades mathématiques, énigmes et défis
-
Anonyme
 par Anonyme » 06 Déc 2009, 12:48
par Anonyme » 06 Déc 2009, 12:48
Doraki a écrit:Oui.
Que vaut a(0)+a(3n) ?
Qu'est-ce qui se passe si a(k) ne prend jamais la valeur 2n ?
Bon j'ai resolu mais je sais pas trop comment ecrire cela en terme mathematique.
Deja a(0)+a(3k)=4n
Si a(k)=a(3k) alors le probleme est resolu.
Donc nous supposerons que a(0)2n . Or la diffrence entre a(k+1) et a(k) est soit 1 soit 0 soit -1 . Donc pour passer d'un nombre inferieur a 2n a un nombre superieur a 2n on doit necessairement passer par 2n.
mais comment ecrire cela rigoureusement de facon mathematique ?
-
poiuytreza
- Membre Naturel
- Messages: 72
- Enregistré le: 22 Avr 2009, 13:40
-
 par poiuytreza » 06 Déc 2009, 13:40
par poiuytreza » 06 Déc 2009, 13:40
Je pense que c'est à peu près suffisant comme ça, mais si tu veux être plus rigoureux, tu peux dire que si a(1) < 2n < a(3n), alors on prend le plus grand k tel que a(k) < 2n. On a alors forcément a(k+1) = 2n.
-
Anonyme
 par Anonyme » 06 Déc 2009, 14:39
par Anonyme » 06 Déc 2009, 14:39
poiuytreza a écrit:Bonjour,
Exercice 5 : ABC est un triangle, I le centre de son cercle inscrit et P le pied de la bissectrice de l'angle en B. On suppose que AP + AB = BC. Montrer que API est isocèle.
Que veut dire cette expression ?
P= (BI) n (AC) ?
-
poiuytreza
- Membre Naturel
- Messages: 72
- Enregistré le: 22 Avr 2009, 13:40
-
 par poiuytreza » 06 Déc 2009, 15:05
par poiuytreza » 06 Déc 2009, 15:05
Oui, le pied de la bissectrice est l'intersection de la bissectrice avec le côté opposé.
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 06 Déc 2009, 16:07
par Matt_01 » 06 Déc 2009, 16:07
Qmath a écrit:Bon j'ai resolu mais je sais pas trop comment ecrire cela en terme mathematique.
Deja a(0)+a(3k)=4n
Si a(k)=a(3k) alors le probleme est resolu.
Donc nous supposerons que a(0)2n . Or la diffrence entre a(k+1) et a(k) est soit 1 soit 0 soit -1 . Donc pour passer d'un nombre inferieur a 2n a un nombre superieur a 2n on doit necessairement passer par 2n.
mais comment ecrire cela rigoureusement de facon mathematique ?
Utiliser la réponse à ma question : l'ensemble que j'ai décrit est nécessairement un intervalle de N. Il reste juste à prouver qu'il contient nécessairement 2n.
-
Anonyme
 par Anonyme » 06 Déc 2009, 17:08
par Anonyme » 06 Déc 2009, 17:08
Matt_01 a écrit:Quelle est la forme de l'ensemble
, k \in [|0,3n|]\})
?
(Cela rejoint l'idée de Doraki).
Meme apres avoir resolu l'exo j'arrive pas a repondre a cette question en fait je crois que je ne comprend pas la question .Pourrais tu donner un exemple de "forme d'un ensemble "?h
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 06 Déc 2009, 20:14
par Matt_01 » 06 Déc 2009, 20:14
Je n'ai pas employé de définition rigoureuse de "forme" qu'on s'entende bien.
Simplement, je demandais à quoi ressemblait cette ensemble (à savoir l'ensemble des valeurs prises par a(k) ).
Du fait que a(k+1)-a(k) vaut +/-1 ou 0, cette ensemble est un intervalle (de N) : chaque valeur entre le min et le max est atteinte.
Après, on a juste à montrer que cas où le max (respectivement le min) est inférieur strictement (respectivement supérieur strictement) à 2n, alors on aboutit à une contradiction : 2n est donc dans l'intervalle et est atteint, ce que l'on voulait montrer.
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 09 Déc 2009, 19:23
par kasmath » 09 Déc 2009, 19:23
les solution du premier exercice
( 0 ;) 2009 ) ;) ( 41 ;) 1476 ) ;)
( 164 ;) 1025 ) ;) ( 369 ;) 656 ) ;)
( 656 ;) 369 ) ;)
( 1025 ;) 164 ) ;) ( 1476 ;) 41 ) ;)
( 2009 ;) 0 )
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 09 Déc 2009, 19:39
par kasmath » 09 Déc 2009, 19:39
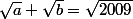
==>
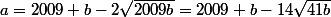
il faut que
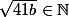
donnant comme hypothése
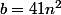
alors
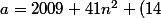41n)
mais
il faut qu'il soit
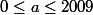
on suite c'est facile de déduire que
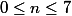
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 11 Déc 2009, 19:23
par kasmath » 11 Déc 2009, 19:23
je crois pour le troisème exercice que
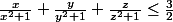
pour x=y=z=1
-
poiuytreza
- Membre Naturel
- Messages: 72
- Enregistré le: 22 Avr 2009, 13:40
-
 par poiuytreza » 11 Déc 2009, 20:29
par poiuytreza » 11 Déc 2009, 20:29
ça c'est le maximum, mais pas de chance, c'est le minimum qu'il faut trouver... :we:
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 12 Déc 2009, 13:35
par kasmath » 12 Déc 2009, 13:35
j'ai oubliée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
