Ln(z) = sqrt(z) ?
18 messages
- Page 1 sur 1
ln(z) = sqrt(z) ?
Bonjour à tous ! Je suis un élève de terminale passionné de mathématiques, et je m'adresse à vous pour résoudre une question que je me suis posée.
Les courbes des fonctions ln(x) et sqrt(x) (j'utilise "sqrt" pour les racines carrées) n'ont pas de point d'intersection sur x appartient à R. Ce qui veut dire qu'il n'existe pas de nombres x appartenants à R tels que ln(x) = sqrt(x).
Mais la question que je me pose est la suivante : y a-t-il un (ou plusieurs) nombres complexes qui vérifient cette équation ?
Voila ce que j'ai trouvé pour l'instant : e^(ln(z)) = e(sqrt(z)) = z
Il s'agirait donc de résoudre e^(sqrt(z)) = z
Je n'ai pas réussi, avec mes connaissances de lycéen, à résoudre ce problème. Bravo à celui qui y arrive, car ça fait plusieurs heures que je suis dessus :ptdr:
Les courbes des fonctions ln(x) et sqrt(x) (j'utilise "sqrt" pour les racines carrées) n'ont pas de point d'intersection sur x appartient à R. Ce qui veut dire qu'il n'existe pas de nombres x appartenants à R tels que ln(x) = sqrt(x).
Mais la question que je me pose est la suivante : y a-t-il un (ou plusieurs) nombres complexes qui vérifient cette équation ?
Voila ce que j'ai trouvé pour l'instant : e^(ln(z)) = e(sqrt(z)) = z
Il s'agirait donc de résoudre e^(sqrt(z)) = z
Je n'ai pas réussi, avec mes connaissances de lycéen, à résoudre ce problème. Bravo à celui qui y arrive, car ça fait plusieurs heures que je suis dessus :ptdr:
Salut !
Si j'ai bien compris, l'équation = \sqrt{z}) n'ayant pas de solutions dans
n'ayant pas de solutions dans  , tu veux essayer de savoir si elle en a dans
, tu veux essayer de savoir si elle en a dans  ?
?
Le problème est que ce n'est pas si simple de considérer les fonctions "logarithme" et "racine carré" dans . Notamment parce que si on garde les même propriétés que le logarithme réel, il peut y avoir plusieurs images pour un même antécédent (cela vient du fait que la fonction
. Notamment parce que si on garde les même propriétés que le logarithme réel, il peut y avoir plusieurs images pour un même antécédent (cela vient du fait que la fonction  est
est  -périodique). Idem pour la racine carrée :
-périodique). Idem pour la racine carrée :  ou
ou 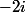 ?
?
Si j'ai bien compris, l'équation
Le problème est que ce n'est pas si simple de considérer les fonctions "logarithme" et "racine carré" dans
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
chan79 a écrit:L'équation (ln(x))²=x admet une unique solution réelle proche de 0,494866
Si on admet que le logarithme complexe coïncide avec le logarithme népérien sur ]0;+[, cette valeur convient.
Bonjour,
Bonne remarque, mais je rappelle que x n'a pas de solutions sur R pour l'équation ln(x) = sqrt(x). On ne peut donc pas se permettre de faire cette étape
chan79 a écrit:Dans, le nombre 1, par exemple, a deux racines carrées qui sont 1 et -1, il me semble
1 et -1 ne sont-ils pas tous les deux réels ? :lol3:
Tout dépend de ce qu'on appelle
On a déjà dit que le problème n'est pas bien posé sous cette forme.
si tu pars du point (x=1, log(x)=0, sqrt(x) = 1) et si tu pars du point (x=1, log(x)=0, sqrt(x)=-1), tu vas avoir deux ensembles de solutions (dans {(x,w,t) / exp(w)=x et t²=x}) différents.
On ne peut pas passer de l'un à l'autre en baladant x dans C*, donc c'est un argument pour dire que même "dans C", ce sont 2 équations différentes (w = exp(w/2) et w = -exp(w/2))
(une reliée au truc dont on est partis sur R, et une autre qui n'y est pas reliée)
On ne peut pas passer de l'un à l'autre en baladant x dans C*, donc c'est un argument pour dire que même "dans C", ce sont 2 équations différentes (w = exp(w/2) et w = -exp(w/2))
(une reliée au truc dont on est partis sur R, et une autre qui n'y est pas reliée)
C'est pas que c'est impossible, c'est un raisonnement par implication.
C'est pour ça que par exemple pour une équation avec racines carrées, lorsque tu élèves au carré les deux membres, tu rajoutes des solutions parasites. Par exemple:
Si x = 4 alors x^2 = 16... mais tu ne repasses pas dans l'autre sens (sauf avec une condition de signe). Si x^2 = 16 alors x = -4 ou 4
Si x = ln(x) alors x = ln(x)^2 mais x = 0.49 ne vérifie clairement pas
x = ln(x) alors x = ln(x)^2 mais x = 0.49 ne vérifie clairement pas  x = ln(x) car les membres ne sont alors pas de même signe.
x = ln(x) car les membres ne sont alors pas de même signe.
C'est pour ça que par exemple pour une équation avec racines carrées, lorsque tu élèves au carré les deux membres, tu rajoutes des solutions parasites. Par exemple:
Si x = 4 alors x^2 = 16... mais tu ne repasses pas dans l'autre sens (sauf avec une condition de signe). Si x^2 = 16 alors x = -4 ou 4
Si
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :


