Retrouver des coefficients d'une moyenne pondérée - débutant

[spawnblade]

Bonjour,

Mon problème est que j'ai des notes et une moyenne de calculée.
Ce que je souhaite, c'est retrouver les coefficients de chacune des notes afin de connaitre les notes à améliorer en priorité pour améliorer la moyenne obtenu.

Dans mon cas, j'ai 15 notes et la moyenne calculée, par exemple :
73,62A + 96,54B + 89,72C + 93,06D + 22,39E + 89,54F + 90,35G + 95,77H + 4,13I + 88,19J + 92,85K + 93,46L + 94,58M + 39,8N + 89,97O / ( A + B+ C + ... + O) = 85,01

Je peux avoir plusieurs exemple bien entendu.

Merci d'avance,

[Dlzlogic]

Bonjour,
C'est un problème assez amusant.
Dans l'absolut, il y a 15 inconnues, donc, il faudrait 15 équations, c'est à dire 15 séries de notes. Il faut ensuite résoudre ce système de 15 équations.
Par ailleurs, comme les coefficients cherchés sont probablement des nombres entiers, il faut être un peu astucieux et les trouver en calculant la somme avant division.

Ceci étant dit, si vous faites des études, je sais c'est obligatoire, c'est pas pour réussir les examens mais pour vous donner une formation. Donc, forcer sur une matière à cause de son coefficient, c'est pas forcément un bon calcul.
Si par hasard, il vous vient un jour l'envie de mettre un exercice dans le forum "Défi", ce n'est pas non plus un bon calcul. Mettez-le dans le forum où il y aura des chances que quelqu'un ait envie de vous aider.

[spawnblade]

En fait non, je ne suis pas étudiant.
Je suis cadre en entreprise et mes études datent de loin ... alors résoudre une équation à 15 inconnues me semble hors de ma portée.
Je cherche à prévoir les résultats d'une application que je n'ai pas créée.
Je sais que les coefficients vont de 0 à 3 et par palier de 0,5.

[Dlzlogic]

En fait non, je ne suis pas étudiant.
Je suis cadre en entreprise et mes études datent de loin ... alors résoudre une équation à 15 inconnues me semble hors de ma portée.
Je cherche à prévoir les résultats d'une application que je n'ai pas créée.
Je sais que les coefficients vont de 0 à 3 et par palier de 0,5.

Bonjour,
Puis que c'est un problème réel, et non un exercice, il vaudrait mieux donner tous les détails.
Par exemple, vous avez moins de 15 relations, ou exactement 15 relations ou plus de 15 relations .
Les coefficient vont de 0 à 3 par paliers de 0.5, ça veut dire qu'il n'y a que 7 valeurs possibles pour les 15 coefficients ou qu'il s'agit d'une simplification acceptable ?
La résolution d'un système de 15 équations linéaires ne présente pas de difficulté particulière.

[Sylviel]

Question complémentaire : pouvez vous donner n'importe quelles valeurs à vos notes ?

[spawnblade]

Je peux avoir plus de 15 équations si besoin, et je peux en avoir 15 tout juste.
Mon nombre d'inconnues est de 15 et pour la valeur possible des coefficients, c'est une info que l'on m'a donné mais je ne sais pas si elle est fiable, à priori oui.

... Pour ce qui est de la difficulté ... elle est toute relative en fonction des compétences de chacun :marteau:

Il faudrait que je puisse répéter l'opération, car en fonction des services, les coefficients ne sont pas les mêmes.

Alors je ne sais pas si avec une feuille de calcul excel ou un programme ou autre ...

[Dlzlogic]

Je me suis mal exprimé concernant la difficulté de résoudre un système de 15 inconnues. Il est bien évident que on ne fait pas ça à la main mais avec un outil de calcul.

Donc, si les solutions pour les coefficients sont limitées au nombre de 7, ce qui me parait bizarre, que se passe-t-il si la résolution donne autre-chose ?
Si vous pouvez avoir plus de 15 équations et qu'on n'en utilise que 15, la solution trouvée ne sera satisfaisante pour celles qui ne sont pas utilisées, ou au contraire, toutes les équations ou presque sont équivalentes, auquel cas le système n'a pas de solution.

Bref, il faut plus de détails, par MP s'il y a un côté confidentiel.

[fatal_error]

salut,

tu poses X ton vecteur colonne de coefficients (A,B,C,...)
et v vecteur colonne des notes que tu as obtenues. (73,62, 96,54, 89,72,...)
le vecteur colonne 1 (1,1,...)
Ton equations s'écrit
v'*X = 85.01 * (1'*X)
soit
(v' - 85.01*1')X = 0
ici, tu vois que si tu fous C,D,...,=0, alors tu peux jouer sur A et B pour avoir 0. Donc c'est pas bon, il faut plus d'equations.
Si tu prends plusieurs equations donc je notes v_i (pour la ieme equation), et r_i le resultat total alors t'as
où 0 est le vecteur colonne (0,0...)
MX = 0
avec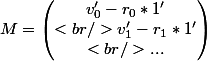
ici r_0 = 85.01

ca revient à chercher le noyau de M (l'ensemble des X qui sont solutions)
http://en.wikipedia.org/wiki/Kernel_%28matrix%29

Du coup tu vas trouver un vecteur X solution (par exemple 1,2,3,4) mais le vecteur (2,4,6,8) sera aussi solution

[spawnblade]

fatal_error,
Comment te dire que tu m'as perdu ? :ptdr:

Dlzlogic,
Non, il n'y a rien de confidentiel, car on ne peut rien en faire ni déduire.

Admettons que j'ai ces 15 équations :
73,72A + 98,61B + 95,99C + 91,5D + 21,7E + 86,39F + 91,3G + 91,43H + 1,03I + 92,17J + 87,49K + 93,2L + 89,4M + 3,04N + 89,05O = 82,55(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

52,51A + 87,97B + 92,21C + 90,76D + 30,84E + 87,49F + 86,51G + 91,4H + 1I + 88,73J + 87,93K + 92,04L + 87,79M + 12,84N + 88,33O = 81,63(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

70,52A + 96,88B + 92,98C + 95,67D + 30,98E + 91,3F + 95,3G + 89,34H + 11,86I + 89,55J + 93,16K + 91,12L + 90,42M + 75,99N + 91,49O = 85,32(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

73,62A + 96,54B + 89,72C + 93,06D + 22,39E + 89,54F + 90,35G + 95,77H + 4,13I + 88,19J + 92,85K + 93,46L + 94,58M + 39,8N + 89,97O = 85,01(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

8,55A + 90,04B + 88,91C + 85,81D + 11,22E + 85,1F + 88,18G + 93,53H + 1I + 84,84J + 92,43K + 88,88L + 16,43M + 1N + 1,1O = 64,71(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

1,86A + 84,53B + 23,17C + 17,16D + 1,78E + 18,98F + 19,48G + 23,1H + 1I + 17,81J + 21,16K + 17,12L + 7,9M + 1N + 1O = 16,26(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

74,13A + 97,63B + 95,03C + 91,73D + 22,63E + 89,78F + 90,39G + 90,52H + 1,01I + 92,17J + 90,86K + 93,2L + 88,51M + 3N + 88,6O = 82,74(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

53,03A + 96,71B + 91,29C + 90,9D + 31,58E + 86,61F + 93,1G + 90,49H + 1I + 88,73J + 87,05K + 91,58L + 86,91M + 12,72N + 88,33O = 81,67(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

69,82A + 95,92B + 92,06C + 94,71D + 30,68E + 91,3F + 94,82G + 97,67H + 11,74I + 92,77J + 93,16K + 90,21L + 89,52M + 75,99N + 90,57O = 86,46(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

72,88A + 95,58B + 88,82C + 92,13D + 22,17E + 91,76F + 89,45G + 95,77H + 4,09I + 91,84J + 92,85K + 92,53L + 94,11M + 39,4N + 89,97O = 85,08(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

8,47A + 89,14B + 88,03C + 84,95D + 11,1E + 87,65F + 87,3G + 93,53H + 1I + 89,23J + 92,43K + 88,88L + 16,57M + 1N + 1,08O = 65,04(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

2,23A + 93,88B + 23,62C + 17,67D + 2,15E + 19,57F + 20,17G + 23,55H + 1I + 17,93J + 21,46K + 21,27L + 8,12M + 1N + 1O = 17,18(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

52,76A + 96,71B + 90,83C + 90,45D + 31,42E + 86,18F + 93,1G + 90,04H + 1I + 88,73J + 86,61K + 91,12L + 86,48M + 12,66N + 88,33O = 81,43(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

69,47A + 95,44B + 91,6C + 94,24D + 30,53E + 90,84F + 94,35G + 97,67H + 11,68I + 92,77J + 93,16K + 89,76L + 89,07M + 79,79N + 90,12O = 86,29(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

72,52A + 95,1B + 98,16C + 91,67D + 22,06E + 91,76F + 89G + 95,29H + 4,07I + 91,84J + 92,85K + 92,07L + 93,64M + 39,2N + 89,97O = 85,21(A+B+C+D+E+F+G+H+I+J+K+L+M+N+O)

[spawnblade]

Sylviel,

Désolé, je n'avais pas vu ta question.
Non, je ne peux modifier les notes pour voir ce que donne le résultat.
En fait je reçois un tableau des notes avec la moyenne pondérée calculée.

merci,

[Dlzlogic]

Bonjour,
Là j'ai besoin d'une idée.
Je pose S = A + B + ... + O
J'introduis donc une seizième inconnue et une 16è équation.
La première équation s'écrira donc
73,72A + 98,61B + 95,99C + 91,5D + 21,7E + 86,39F + 91,3G + 91,43H + 1,03I + 92,17J + 87,49K + 93,2L + 89,4M + 3,04N + 89,05O -82.55*S = 0
et la dernière (16è)
A + B + C + ... + O - S = 0
La solution que je trouve pour toutes les valeurs est 0 (zéro)
En fait comme il n'y a pas de constante, à droite du signe '=', la solution = 0 est la seule possible.

Donc, ma question concernant des détails supplémentaire sur l'origine de ces valeurs reste d'actualité.

[Dlzlogic]

J'ai trouvé.
En fait, en matière de poids, la seule chose importante est les rapports les une par rapport aux autres.
Donc, Je "décide" que la somme des poins est 1, j'aurais pu prendre 100 ou 1000.
Les solutions
-0.12 -0.00 0.03 -0.21 -0.16 0.02 0.15 0.16 0.68 0.05 0.28 0.20 0.22 -0.06 0.15

(Le 0.00 n'est pas zéro, mais petit négatif)

En prenant 100, ça donne ça
Les solutions
-12.25 -0.35 3.34 -20.54 -16.48 1.95 15.37 16.19 68.34 4.75 28.47 19.75 21.53 -6.27 14.72

[spawnblade]

Donc, ma question concernant des détails supplémentaire sur l'origine de ces valeurs reste d'actualité.

Je ne sais pas quels éléments je pourrais te donner en plus.
Une note est attribué dans chacun des 15 domaines.
Chaque domaine à un coefficient.

En réalité, je dis que je peux avoir plusieurs équations, car les notes évoluent chaque jour, donc à la base j'ai 5 équations et le lendemain les notes ayant évolués j'ai de nouveau 5 équations, ainsi de suite.

[Dlzlogic]

Je ne sais pas quels éléments je pourrais te donner en plus.
Une note est attribué dans chacun des 15 domaines.
Chaque domaine à un coefficient.

En réalité, je dis que je peux avoir plusieurs équations, car les notes évoluent chaque jour, donc à la base j'ai 5 équations et le lendemain les notes ayant évolués j'ai de nouveau 5 équations, ainsi de suite.

Ce qui parait un peu étonnant c'est qu'il y a des coefficients négatifs. En matière de notation, c'est assez rare, sauf si certains coefficients correspondent à "BON" et d'autres à "MAUVAIS".
Donc chaque jour il y a 5 nouvelles équations qui remplacent les 5 équations de 4 jours avant, puisque chaque jour, il y a 15 équations.
J'ai toujours pas compris ce que vous attendez de nous.
Si c'est pour le faire avec un tableur, il faudra le demander à quelqu'un d'autre. Moi, les tableurs, j'aime pas.

Ce qui serait intéressant à calculer, c'est ce que seraient ces coefficients datant d'une quinzaine de jours. Serait-ce même ? En fait je suis presque sûr que non et que le problème posé n'est pas exactement celui-là.

[spawnblade]

J'ai trouvé.
En fait, en matière de poids, la seule chose importante est les rapports les une par rapport aux autres.
Donc, Je "décide" que la somme des poins est 1, j'aurais pu prendre 100 ou 1000.
Les solutions
-0.12 -0.00 0.03 -0.21 -0.16 0.02 0.15 0.16 0.68 0.05 0.28 0.20 0.22 -0.06 0.15

(Le 0.00 n'est pas zéro, mais petit négatif)

En prenant 100, ça donne ça
Les solutions
-12.25 -0.35 3.34 -20.54 -16.48 1.95 15.37 16.19 68.34 4.75 28.47 19.75 21.53 -6.27 14.72

Donc si je comprends bien, on obtiens des poids de coefficient ?
C'est un peu ce que j'ai obtenu sur excel avec la fonction droitereg sur mes 15 équations.
Mais qu'est ce que j'en fais ensuite ?
Car ce ne me donne pas les coefficients. Et quand je vois un poids négatif, est ce que cela implique que mon coefficient est négatif ?

En tout cas, merci pour votre aide ! C'est sympa ! :lol3:

[Dlzlogic]

Je ne sais pas ce que vous appelez "poids" ou "coefficient". La seule chose que je peux vous dire, c'est qu'étant donné les 15 équations fournies, les 15 inconnues sont celles que j'ai indiquées, à un facteur multiplicatif près.

[spawnblade]

Si je comprends bien, quand tu poses S = A + B + ... + O
Pour trouver ces résultats, tu considère que S = 1 ?

[Dlzlogic]

Si je comprends bien, quand tu poses S = A + B + ... + O
Pour trouver ces résultats, tu considère que S = 1 ?

C'est à peu près ça. Les poids A, B, C etc sont tels que la somme des quantités "valeur * poids" donne une quantité "pondérée".
Si on multiplie ou divise chaque poids par un même facteur, on ne change rien au résultat.
Je dirais que, S, la somme des poids, est le poids de référence. On peut prendre n'importe quoi, pourvu qu'on le sache.
Mais dans le cas présent le terme "Poids" n'est pas très adapté, puisque habituellement un poids est positif.

[spawnblade]

Oui, c'est bien ça qui m’embête. C'est de trouver des valeurs négatives ...

[Dlzlogic]

Oui, c'est bien ça qui m’embête. C'est de trouver des valeurs négatives ...

Je veux bien vous dire mon avis, mais il faudrait que je sache de quoi il s'agit.
S'il s'agit de maths pures où les valeurs n'ont pas de réalité physique, alors vous avez votre réponse.
Si les valeurs concernées représentent quelque-chose, je ne peux pas plus vous aider tant que je ne sais pas de quoi il s'agit.

En fait une question que je me pose : quelle est l'évolution des poids, puisque je suis persuadé qu'ils bougent avec le temps. Je suis sûr que l'examen de plusieurs jours consécutifs, et dans l'ordre permettrait de m'éclairer.
Le problème admet une solution si on a exactement 15 équations indépendantes. Or vous m'avez dit que chaque jour apportait 5 équations, donc il n'y a aucune raison que les paramètres restent constants d'un jour à l'autre. Ce qui a pour conséquence que la résolution du système de 15 équation n'a pas beaucoup de sens.
Il serait beaucoup plus intéressant de résoudre un système d'au moins une trentaine d'équations.