Petit exo sympa
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 23 Juil 2006, 18:50
par nekros » 23 Juil 2006, 18:50
Bonsoir,
Avant de partir en vacances, un petit exo sympa :
Soient

de
dans
de classe

et

de
dans
telle que

.
On suppose que :
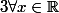
,
+xg(x)f'(x)+f(x)=0) Démontrer que
Démontrer que  est bornée.
est bornée.Bonne réflexion.
Thomas G :zen:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 23 Juil 2006, 22:47
par nekros » 23 Juil 2006, 22:47
Personne ?
Les exos que je propose n'ont vraiment pas de succès en ce moment :cry:
Thomas G :zen:
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 23 Juil 2006, 23:07
par Sdec25 » 23 Juil 2006, 23:07
Peut-être qu'ils sont trop difficiles ?
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 23 Juil 2006, 23:08
par raptor77 » 23 Juil 2006, 23:08
ou pas assez interressant?
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 23 Juil 2006, 23:12
par nekros » 23 Juil 2006, 23:12
raptor77 a écrit:ou pas assez interressant?
Vraiment sympa... :hum:
Thomas G :zen:
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 23 Juil 2006, 23:13
par raptor77 » 23 Juil 2006, 23:13
Mais je rigolais , un peu d'humour voyons.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 23 Juil 2006, 23:16
par nekros » 23 Juil 2006, 23:16
Ok, désolé !
Mais je suis sûr que tu peux le résoudre !
Sdec idem.
Considère
=(f(x))^2+(f'(x))^2)
Thomas G :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités