Obtus avec un s, aigu sans s

par **nodgim** » 30 Aoû 2008, 09:33

Mis à part ce petit rappel orthographique, un triangle avec un angle obtus peut il être partagé en triangles à angles strictement aigus ? :arf:

par **guigui51250** » 30 Aoû 2008, 09:45

nodgim a écrit:Mis à part ce petit rappel orthographique, un triangle avec un angle obtus peut il être partagé en triangles à angles strictement aigus ? :arf:

j'ai pas compris ça veut dire quoi "partagé avec"?

par **nodgim** » 30 Aoû 2008, 09:48

guigui51250 a écrit:j'ai pas compris ça veut dire quoi "partagé avec"?

Je ne sais pas, qui a écrit "partagé avec" ? :doh:

par **Edward** » 30 Aoû 2008, 09:49

Si on prend un triangle ABC obtus en A, on peut trouver un point D appartenant à BC tel que ABD soit composé uniquement d'angles aigus, ce qui ne sera pas le cas pour ACD : (mes)ADC = 180-mes(ADB) > 90.
Le problème se repete ainsi à l'infini, donc je dirais non ^^.

par **nodgim** » 30 Aoû 2008, 09:52

Edward a écrit:Si on prend un triangle ABC obtu en A, on peut trouver un point D appartenant à BC tel que ABD soit composé uniquement d'angles aigus, ce qui ne sera pas le cas pour ACD : (mes)ADC = 180-mes(ADB) > 90.
Le problème se repete ainsi à l'infini, donc je dirais non ^^.

A quoi cela sert il que je fasse un rappel de l'orthographe de "obtus" ? :mur:

par **Edward** » 30 Aoû 2008, 09:55

nodgim a écrit:A quoi cela sert il que je fasse un rappel de l'orthographe de "obtus" ? :mur:

Oups dsl j'ai modifié l'erreur. T'a raison les gens font de plus en plus de fautes d'orthographe en maths de nos jours.

par **guigui51250** » 30 Aoû 2008, 09:56

nodgim a écrit:Je ne sais pas, qui a écrit "partagé avec" ? :doh:

mdrr j'ai mal compris je croyais que tu avais écrit partagé avec des triangles à angles strictement aigu :mur: :mur: :mur:

par **nodgim** » 30 Aoû 2008, 10:00

Edward a écrit:Si on prend un triangle ABC obtus en A, on peut trouver un point D appartenant à BC tel que ABD soit composé uniquement d'angles aigus, ce qui ne sera pas le cas pour ACD : (mes)ADC = 180-mes(ADB) > 90.
Le problème se repete ainsi à l'infini, donc je dirais non ^^.

Non, on peut faire beaucoup mieux....

par **lapras** » 30 Aoû 2008, 10:44

On ne peut pas avec strictement aigus mais on peut avec aigus. (sauf erreur !)

par **nodgim** » 30 Aoû 2008, 12:23

lapras a écrit:On ne peut pas avec strictement aigus mais on peut avec aigus. (sauf erreur !)

Sur quoi se fonde ton assertion ?

par **Imod** » 30 Aoû 2008, 22:41

C'est bizarre , j'ai vu ce problème et sa solution récemment et je n'ai rien noté tant tout ça semblait évident . Je ne retrouve plus rien :marteau:

Imod

par **nodgim** » 31 Aoû 2008, 06:43

Je ne savais pas qu'il était connu, je l'ai cherché seul. Par contre, il m'a été inspiré par une autre question: partager un carré en 8 triangles à angles strictement aigus. Pas simple non plus celui là.

par **Imod** » 31 Aoû 2008, 16:44

Un lien vers le problème que tu as évoqué : Découpage d'un carré

J'ai une solution pour le triangle obtusangle en 7 ou 8 morceaux mais il faut encore que je peaufine ma démo car apparemment il y a plusieurs cas .

Imod

par **Imod** » 31 Aoû 2008, 18:14

Allons-y :

On note

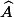
l'angle obtus du triange

. Si

et

alors le pavage ci-dessus donne la réponse (

est le centre du cercle inscrit dans

) . Si par exemple

alors on coupe ABC en deux triangles

et

avec

et on découpe

comme ci-dessus .

Imod

par **nodgim** » 01 Sep 2008, 17:26

J'ai trouvé une solution légèrement différente, mais toujours avec un pentagone central : découpe du triangle en 2 triangles rectangles selon la petite hauteur. Joindre le point bas de la hauteur avec les milieux des cotés opposés pour obtenir des triangles isocèles, dont 2 obtuangles. Alors, on réussit toujours à former dans chacun d'eux un pentagone composés de 5 triangles strictement acutangles, facilement démontrables en profitant de la symétrie.

Obtus avec un s, aigu sans s

Obtus avec un s, aigu sans s

Qui est en ligne