Numéros spéciaux
Olympiades mathématiques, énigmes et défis
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 02 Oct 2016, 06:25
par Dacu » 02 Oct 2016, 06:25
Bon matin,
Trouver tous les numéros
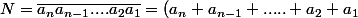^n)
.
----------------------------------
Exemples:
81=(8+1)^2
512=(5+1+2)^3
2401=(2+4+0+1)^4
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 02 Oct 2016, 07:55
par anthony_unac » 02 Oct 2016, 07:55
Bonjour,
Voila un joli défi

Je tente de formaliser le problème à l'aide du multinôme de Newton :
(1)^{n}=\sum _{{k_{1}+k_{2}+k_{3}+\ldots +k_{n}=n}}{n \choose k_{1},k_{2},k_{3},\dots ,k_{n}}a_{1}^{{k_{1}}}a_{2}^{{k_{2}}}a_{3}^{{k_{3}}}\dots a_{n}^{{k_{n}}}={\frac {n!}{k_{1}!k_{2}!k_{3}!\dots k_{n}!}}a_{1}^{{k_{1}}}a_{2}^{{k_{2}}}a_{3}^{{k_{3}}}\dots a_{n}^{{k_{n}}}.)
Je réécris le numéro sous forme d'un développement en puissance de dix :
(2) 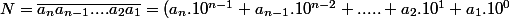)
Il ne reste "plus qu'à" résoudre
(1)=(2)Mais cette équation est trop rude pour moi (je me perds dans les indices


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Oct 2016, 08:33
par zygomatique » 02 Oct 2016, 08:33
salut
une équation et n inconnues ...
je ne pense pas qu'on puisse résoudre de façon générale cette équation polynomiale de degré n ...
on peut cependant remarquer que N (donc a_1) et

ont même parité ...
donc que

est pair ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 02 Oct 2016, 10:20
par Lostounet » 02 Oct 2016, 10:20
Pour le cas le plus simple
(10x+y)=(x+y)^2
10x+y=x^2+2xy+y^2
X^2+y^2-y
Donc x est pair. Et la somme (x+y) ne peut excéder 10
Plus qu'à tester
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 02 Oct 2016, 11:07
par nodgim » 02 Oct 2016, 11:07
On a
10^(n-1) < k^n < 10 ^n qui donne
10^(1-1/n) < k < 10
Et assez vite, il ne reste que k = 9 comme solution.
(9 ^ n) a pour somme de chiffres un multiple de 9, mais on veut obtenir une puissance de 9 dont la somme des chiffres est exactement 9.
On sait obtenir une puissance de n'importe quel nombre (premier avec 10) dont le résultat donnera un nombre commençant par ce qu'on veut (10000...par exemple) et finissant par.... 00001. Mais on ne sait pas ce qu'il se passe au milieu du nombre. Mais il y a très très peu de chances qu'on puisse obtenir un tel nombre. Alors je dirais qu'il n'y a pas d'autres cas que ceux trouvés par Cadu.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 02 Oct 2016, 11:28
par chan79 » 02 Oct 2016, 11:28
salut
Effectivement, c'est dur de trouver un autre exemple, sauf le cas trivial :


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Oct 2016, 11:33
par zygomatique » 02 Oct 2016, 11:33
nodjim : c'est quoi ton k ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 02 Oct 2016, 11:55
par nodgim » 02 Oct 2016, 11:55
k est la somme des chiffres du nombre qui vérifie l'égalité. L'inégalité décrite vient du fait que N possède exactement n chiffres.
En fait, on peut terminer l'histoire en remarquant que 10 ^(21/22) > 9. Et donc au delà de n=21, il ne peut plus y avoir de solution. Et en deçà, il n'y en a pas d'autres que celles citées.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 03 Oct 2016, 05:18
par Dacu » 03 Oct 2016, 05:18
nodgim a écrit:k est la somme des chiffres du nombre qui vérifie l'égalité. L'inégalité décrite vient du fait que N possède exactement n chiffres.
En fait, on peut terminer l'histoire en remarquant que 10 ^(21/22) > 9. Et donc au delà de n=21, il ne peut plus y avoir de solution. Et en deçà, il n'y en a pas d'autres que celles citées.
Bon matin,
Je pense que plus restrictive

Et alors , quelles d'autres valeurs peuvent avoir

?
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 03 Oct 2016, 05:22
par Dacu » 03 Oct 2016, 05:22
chan79 a écrit:salut
Effectivement, c'est dur de trouver un autre exemple, sauf le cas trivial :

Bon matin,
Autres cas triviaux sont

où

.
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 03 Oct 2016, 09:36
par nodgim » 03 Oct 2016, 09:36
Dacu a écrit: nodgim a écrit:k est la somme des chiffres du nombre qui vérifie l'égalité. L'inégalité décrite vient du fait que N possède exactement n chiffres.
En fait, on peut terminer l'histoire en remarquant que 10 ^(21/22) > 9. Et donc au delà de n=21, il ne peut plus y avoir de solution. Et en deçà, il n'y en a pas d'autres que celles citées.
Bon matin,
Je pense que plus restrictive

Et alors , quelles d'autres valeurs peuvent avoir

?
Cordialement!
Dacu, il ne peut pas y avoir des solutions supplémentaires dans un intervalle plus restrictif qu'un intervalle donné !
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 04 Oct 2016, 14:21
par Dacu » 04 Oct 2016, 14:21
nodgim a écrit: Dacu a écrit: nodgim a écrit:k est la somme des chiffres du nombre qui vérifie l'égalité. L'inégalité décrite vient du fait que N possède exactement n chiffres.
En fait, on peut terminer l'histoire en remarquant que 10 ^(21/22) > 9. Et donc au delà de n=21, il ne peut plus y avoir de solution. Et en deçà, il n'y en a pas d'autres que celles citées.
Bon matin,
Je pense que plus restrictive

Et alors , quelles d'autres valeurs peuvent avoir

?
Cordialement!
Dacu, il ne peut pas y avoir des solutions supplémentaires dans un intervalle plus restrictif qu'un intervalle donné !
Bonjour,
En fait, je voulais dire que je pense qu'il est plus sûr de considérer

.
------------------------------------------
Le problème n'a pas encore été résolu , parce que nous ne savons pas si plus sont oui ou non d'autres numéros qui vérifient la condition imposée.
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 04 Oct 2016, 16:30
par nodgim » 04 Oct 2016, 16:30
Bonjour,
En fait, je voulais dire que je pense qu'il est plus sûr de considérer

.
------------------------------------------
Le problème n'a pas encore été résolu , parce que nous ne savons pas si plus sont oui ou non d'autres numéros qui vérifient la condition imposée.
Cordialement!
Comprends pas. Je donne un intervalle plus large que le tien, et tu dis que le tien est plus sûr ? En quoi est il plus sûr ? Ce que j'ai écrit dans mon inégalité, c'est que k^n est un nombre de n chiffres. C'est bien une contrainte de l'énoncé, non ?
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 05 Oct 2016, 06:13
par Dacu » 05 Oct 2016, 06:13
nodgim a écrit:Comprends pas. Je donne un intervalle plus large que le tien, et tu dis que le tien est plus sûr ? En quoi est il plus sûr ? Ce que j'ai écrit dans mon inégalité, c'est que k^n est un nombre de n chiffres. C'est bien une contrainte de l'énoncé, non ?
Bon matin,
Sans infraction, mais votre gamme sur la gauche est trop large.Votre gamme , à gauche , est valide pour
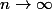
...

Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 05 Oct 2016, 07:25
par nodgim » 05 Oct 2016, 07:25
Ben non, justement. Et je l'ai déjà écrit.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités

?
?