Cinq numéros
22 messages
- Page 1 sur 2 - 1, 2
Cinq numéros
Bonjour à tous,
Un problème de 5eme classe:
Trouver:
a) le plus grand nombre naturel qui est le plus grand diviseur commun de cinq naturels numéros différents de zéro ayant somme 2016;
b) le plus petit nombre qui est le plus petit multiple commun de cinq naturels numéros différents de zéro ayant somme 2016.
Cordialement!
Un problème de 5eme classe:
Trouver:
a) le plus grand nombre naturel qui est le plus grand diviseur commun de cinq naturels numéros différents de zéro ayant somme 2016;
b) le plus petit nombre qui est le plus petit multiple commun de cinq naturels numéros différents de zéro ayant somme 2016.
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Cinq numéros
en cinquième, hum, my god!
bon ben pour le a)
ce nombre fois (1+2+3+4+5) = 2016, je peux pas faire moins que le 15 pour qu'ils soient différents,
sauf que y a pas de multiple de 5, donc faut passer à somme des 5 trucs fait 16.
et le a) devient 2016/16
et là on a regagné 20 places PISA!
bon ben pour le a)
ce nombre fois (1+2+3+4+5) = 2016, je peux pas faire moins que le 15 pour qu'ils soient différents,
sauf que y a pas de multiple de 5, donc faut passer à somme des 5 trucs fait 16.
et le a) devient 2016/16
et là on a regagné 20 places PISA!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Cinq numéros
salut
le pgcd cherché divise 5 nombres dont la somme est 2016 donc il divise 2016
336 est le pgcd de 336, 336, 336 , 336 et 672
336+336+336+336+672=2016
le pgcd cherché divise 5 nombres dont la somme est 2016 donc il divise 2016
336 est le pgcd de 336, 336, 336 , 336 et 672
336+336+336+336+672=2016
Re: Cinq numéros
chan79 a écrit:salut
le pgcd cherché divise 5 nombres dont la somme est 2016 donc il divise 2016
336 est le pgcd de 336, 336, 336 , 336 et 672
336+336+336+336+672=2016
Salut,
Comment vous avez calculé les numéros 336,336,336,336 et 672?
Et le ppmc?
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Cinq numéros
Bonjour à tous,
Mon raisonnement:
a) Soit le plus grand nombre naturel qui est le plus grand diviseur commun , alors nous pouvons écrire:
le plus grand nombre naturel qui est le plus grand diviseur commun , alors nous pouvons écrire:
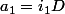 ,
, 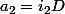 ,
, 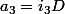 ,
, 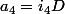 et
et 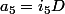 où
où 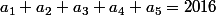 avec
avec  et alors
et alors  .Parce que
.Parce que  doit être le plus grand nombre naturel et
doit être le plus grand nombre naturel et  alors la somme
alors la somme  doit être minimum , ce qui signifie que
doit être minimum , ce qui signifie que  et
et 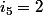 et il résulte que
et il résulte que 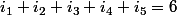 et
et  .
.
b) Soit le plus petit nombre naturel qui est le plus petit multiple commun , alors nous pouvons écrire:
le plus petit nombre naturel qui est le plus petit multiple commun , alors nous pouvons écrire:
 ,
,  ,
, 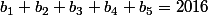 et
et  .Parce que
.Parce que  doit être le plus petit nombre naturel et
doit être le plus petit nombre naturel et  alors la somme
alors la somme  doit être maximum , ce qui signifie que
doit être maximum , ce qui signifie que  et
et  et il résulte que
et il résulte que  et
et  .
.
Cordialement!
Mon raisonnement:
a) Soit
b) Soit
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Cinq numéros
chan79 a écrit:le PPCM de 448, 448, 448, 448 et 224 est 448
448+448+448+448+224=2016
Salut,
Je ne comprends pas!
Merci beaucoup!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Cinq numéros
chan79 a écrit:siet
et il résulte que
et
.
Bonsoir,
J'ai révisé mon raisonnement et je comprends votre raisonnement! Vous avez tout à fait raison!Je pensais mal que
Merci beaucoup!Bonne soirée!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Cinq numéros
sauf que :
1/ à priori on travaille avec des entiers
2/ il est demandé cinq entiers distincts (pour les deux questions)
...
1/ à priori on travaille avec des entiers
2/ il est demandé cinq entiers distincts (pour les deux questions)
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Cinq numéros
j'ai compris qu'on demande cinq entiers naturels différents de 0
pour la question a):
336 est le pgcd de 336, 336, 336 , 336 et 672
pour la question b):
448 est le PPCM de 448, 448, 448, 448 et 224
pour la question a):
336 est le pgcd de 336, 336, 336 , 336 et 672
pour la question b):
448 est le PPCM de 448, 448, 448, 448 et 224
Re: Cinq numéros
Bonjour à tous,
Dans le cas b) , le raisonnement correct est:
b) Soit le plus petit nombre naturel qui est le plus petit multiple commun , alors nous pouvons écrire:
le plus petit nombre naturel qui est le plus petit multiple commun , alors nous pouvons écrire:
 ,
,  ,
, 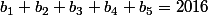 et
et  .Parce que
.Parce que  doit être le plus petit nombre naturel alors la somme
doit être le plus petit nombre naturel alors la somme  doit être maximum , ce qui signifie que
doit être maximum , ce qui signifie que  et
et  et il résulte que
et il résulte que  et
et  .
.
Remarque:
1) ne peut pas être égal avec
ne peut pas être égal avec  parce que
parce que  serait fractionnaire
serait fractionnaire
2) ne peut pas être ne peut pas être plus grand que
ne peut pas être ne peut pas être plus grand que  parce que
parce que  doit être le plus petit nombre naturel et dans le cas
doit être le plus petit nombre naturel et dans le cas  on obtient que
on obtient que  .
.
Cordialement!
Dans le cas b) , le raisonnement correct est:
b) Soit
Remarque:
1)
2)
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Cinq numéros
comme zygomatique j'avais lu "différents" tout court,
lecture trop rapide ou bien rajout secondaire de "différents de zéro"???
lecture trop rapide ou bien rajout secondaire de "différents de zéro"???
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Cinq numéros
Pour le a) j'avais fait ça: (proche de ce qu'à fait Dacu)
Il s'agit donc de trouver 5 entiers naturels, tous non nuls, de somme 2016, tels que leur PGCD soit maximum.
Ce PGCD divise donc 2016.
Les plus grands diviseurs de 2016 sont 288, 336, 504, 672, 1008, 2016
Essayons 288
Les 5 nombres sont de la forme 288a, 288b, 288c, 288d et 288e
En les ajoutant
288(a+b+c+d+e)=2016
a+b+c+d+e=7
on a des possibilités, par exemple a=b=c=1 et d=e=2
Les cinq nombres sont 288, 288, 288, 576 et 576
Essayons 336
on arrive à
336(a+b+c+d+e)=2016
a+b+c+d+e=6
si on ne tient pas compte de l'ordre, on a 1 possibilité
a=b=c=d=1 et e=2
Les cinq nombres sont 336,336,336,336,672
Essayons 504
on arrive à
a+b+c+d+e=4
impossible car les cinq nombres doivent être non nuls.
Avec 672, 1008 et 2016, ça ne va pas non plus.
Le pgcd demandé est 336.
Il s'agit donc de trouver 5 entiers naturels, tous non nuls, de somme 2016, tels que leur PGCD soit maximum.
Ce PGCD divise donc 2016.
Les plus grands diviseurs de 2016 sont 288, 336, 504, 672, 1008, 2016
Essayons 288
Les 5 nombres sont de la forme 288a, 288b, 288c, 288d et 288e
En les ajoutant
288(a+b+c+d+e)=2016
a+b+c+d+e=7
on a des possibilités, par exemple a=b=c=1 et d=e=2
Les cinq nombres sont 288, 288, 288, 576 et 576
Essayons 336
on arrive à
336(a+b+c+d+e)=2016
a+b+c+d+e=6
si on ne tient pas compte de l'ordre, on a 1 possibilité
a=b=c=d=1 et e=2
Les cinq nombres sont 336,336,336,336,672
Essayons 504
on arrive à
a+b+c+d+e=4
impossible car les cinq nombres doivent être non nuls.
Avec 672, 1008 et 2016, ça ne va pas non plus.
Le pgcd demandé est 336.
Re: Cinq numéros
euh,
5 nombres : PGCD xa, PGCDxb, PGCDXc, PGCDxd,PGCDxe
somme des 5 nombres = 2016
si PGCD en facteur commun
PGCD x (a+b+c+d+e) = 2016
PGCD max quand (a+b+c+d+e) minimimal
pour des entiers non nuls le minimum est à 1, ce qui donnerait 5
sauf que 5 ne divise pas 2016
donc on passe à minimal = 6 qui divise 2016
PGCD max = 2016/6
Pour des nombres différents, le cas que j'avais traité:
minimal = 1+2+3+4+5 = 15
marche pas idem
on passe à 16
PGCD max = 2016/16
5 nombres : PGCD xa, PGCDxb, PGCDXc, PGCDxd,PGCDxe
somme des 5 nombres = 2016
si PGCD en facteur commun
PGCD x (a+b+c+d+e) = 2016
PGCD max quand (a+b+c+d+e) minimimal
pour des entiers non nuls le minimum est à 1, ce qui donnerait 5
sauf que 5 ne divise pas 2016
donc on passe à minimal = 6 qui divise 2016
PGCD max = 2016/6
Pour des nombres différents, le cas que j'avais traité:
minimal = 1+2+3+4+5 = 15
marche pas idem
on passe à 16
PGCD max = 2016/16
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Cinq numéros
salut beagle
oui, ce que tu as fait est plus concis
Dacu a fait à peu près pareil
je me suis compliqué la vie
Bonne semaine
A+
oui, ce que tu as fait est plus concis
Dacu a fait à peu près pareil
je me suis compliqué la vie
Bonne semaine
A+
Re: Cinq numéros
salut chan79,
tu as déplacé le fil qui était au forum collège,
tu sais si "de zéro" a été rajouté ultérieurement?
tu as déplacé le fil qui était au forum collège,
tu sais si "de zéro" a été rajouté ultérieurement?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Cinq numéros
je ne sais pas
Pour ma part, je n'ai pas fait de modif
Dacu voudra bien nous informer, je pense
Pour ma part, je n'ai pas fait de modif
Dacu voudra bien nous informer, je pense
Re: Cinq numéros
chan79 a écrit:je ne sais pas
Pour ma part, je n'ai pas fait de modif
Dacu voudra bien nous informer, je pense
Salut,
Jamais je ne l'ai pas changé l'énoncé du problème!Vous avez résolu le problème correctement!
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Cinq numéros
Ok lu trop vite alors.
Comme tous ces élèves qui foncent tète baissée après avoir lu les 3 premiers mots ...ah, ah!
Comme tous ces élèves qui foncent tète baissée après avoir lu les 3 premiers mots ...ah, ah!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
