est un nombre entier.
Nombres entiers positifs
15 messages
- Page 1 sur 1
nombres entiers positifs
Déterminez toutes les paires ) des nombres positifs entiers tels que
des nombres positifs entiers tels que
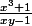
est un nombre entier.
est un nombre entier.
Re: nombres entiers positifs
Be careful : for french mathematicians a "positive" number X mean a number such thatalice02 a écrit:no is good. Because the numbers must be
See for exemple the "bible" of the (french) mathematics (but not only French...), N.Bourbaki where you can read
"0 is the only number witch is both positive and negative".
And if you want to understand why there is such a difference, it's because in France, the only definition we have for a (binary) partial order is "Reflexive + Transitive + Antisymetric" so
In English, there are two definitions : one for "non strict partial order" and one for "strict partial order".
And if I say to be carreful, it's because it's the same problem for other partials orders such as "to be a subset of" : When a french mathematician write
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: nombres entiers positifs
Ah ok Ben314, I didn't know it.
But someone can post a resolution?
Thanks
But someone can post a resolution?
Thanks
Re: nombres entiers positifs
Sinon, pour tout 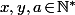
\ \Leftrightarrow\ \left\{\begin{matrix}b\!=\!ay-x^2\cr 1\!+\!a\!=\!bx\ \ \end{matrix}\right.\ \Leftrightarrow\ \left\{\begin{matrix}a\!=\!bx\!-\!1\ \ \ \ \ \ \ \ \ \ \ \cr b\!=\!(bx\!-\!1)y\!-\!x^2\ \ \end{matrix}\right.) avec
avec 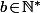 (sinon
(sinon 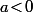 )
)
Il faut donc résoudre\!=\!0) .
.
Le discriminant (en )
) ^2\!-\!4(b\!+\!y)) doit être le carré d'un entier
doit être le carré d'un entier 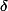 .
.
- On a évidement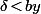 vu que
vu que ^2) .
.
- Mais d'un autre coté, on a la série d'équivalences suivantes (modulo que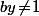 ) :
) :
^2\!<\!\Delta\ \Leftrightarrow\ -4by\!+\!4\!<\!-\!4(b\!+\!y)\ \Leftrightarrow\ (b\!-\!1)(y\!-\!1)\!>\!2) .
.
Ce qui signifie que, si(y\!-\!1)\!>\!2) , la seule possibilité pour
, la seule possibilité pour 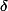 est
est  sauf que cette dernière équation conduit (en l'élevant au carré) à
sauf que cette dernière équation conduit (en l'élevant au carré) à \!=\!-\!2by\!+\!1) clairement sans solution (problème de parité).
clairement sans solution (problème de parité).
Reste à traiter les cas où(y\!-\!1)\!\leq\!2) (c.f. EDIT çi dessous)
(c.f. EDIT çi dessous)
P.S. : Il y a surement d'autres méthodes un peu moins "rustres" (par exemple utilisant la divisibilité)...
EDIT :
- Pour y=1, l'unique solution est b=5 (et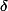 =1) qui conduit à x=2 ou bien x=3.
=1) qui conduit à x=2 ou bien x=3.
- Par symétrie, pour b=1, l'unique solution est y=5 qui conduit à x=2 ou bien x=3.
- Pour b=y=2 l'unique solution (double) est x=2
- Pour b=2; y=3 on a deux solutions x=1 ou bien x=5.
- Par symétrie, pour b=3; y=2 on a aussi deux solutions x=1 ou bien x=5.
Donc sauf erreur 9 solutions : (x,y)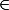 { (1;2) ; (1;3) ; (2;1) ; (2;2) ; (2;5) ; (3;1) ; (3;5) ; (5;2) ; (5;3) }
{ (1;2) ; (1;3) ; (2;1) ; (2;2) ; (2;5) ; (3;1) ; (3;5) ; (5;2) ; (5;3) }
Il faut donc résoudre
Le discriminant (en
- On a évidement
- Mais d'un autre coté, on a la série d'équivalences suivantes (modulo que
Ce qui signifie que, si
Reste à traiter les cas où
P.S. : Il y a surement d'autres méthodes un peu moins "rustres" (par exemple utilisant la divisibilité)...
EDIT :
- Pour y=1, l'unique solution est b=5 (et
- Par symétrie, pour b=1, l'unique solution est y=5 qui conduit à x=2 ou bien x=3.
- Pour b=y=2 l'unique solution (double) est x=2
- Pour b=2; y=3 on a deux solutions x=1 ou bien x=5.
- Par symétrie, pour b=3; y=2 on a aussi deux solutions x=1 ou bien x=5.
Donc sauf erreur 9 solutions : (x,y)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: nombres entiers positifs
Lostounet, il est très fort en anglais...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: nombres entiers positifs
Lostounet, il est très fort en anglais...
Translating Ben's post:
Okay, other than that, for all
We therefore have to solve the quadratic equation
Computing its discriminant, we get:
- Obviously
- On the other hand, we have the following series of logical equivalences (granted that
Which means that, if
The only cases left to study are
P.S. : I'm sure there are other less "crude" methods (using divisibility properties of the integers for example)
EDIT :
- For y=1, the only solution is b=5 (and
- By symmetry, for b=1, the only solution is y=5 which leads us to x=2 or x=3.
- For b=y=2, the only (repeated) solution is x=2
- Take b=2; y=3 we have two solutions x=1 or x=5.
- By symmetry, for b=3; y=2 we also have two solutions x=1 or x=5.
So basically we have 9 solutions : (x,y)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: nombres entiers positifs
Merci Lostounet.... 

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: nombres entiers positifs
Lostounet a écrit:Lostounet, il est très fort en anglais...
Translating Ben's post:
Okay, other than that, for allwith
(otherwise
)
We therefore have to solve the quadratic equation.
Computing its discriminant, we get: (en)
which has to be the square of some integer
.
- Obviouslysince
.
- On the other hand, we have the following series of logical equivalences (granted that) :
.
Which means that, if, the only possibility for
is
however, squaring both sides of the last equation yields
which clearly has no solutions (parity incompatibility).
The only cases left to study are(look below)
P.S. : I'm sure there are other less "crude" methods (using divisibility properties of the integers for example)
EDIT :
- For y=1, the only solution is b=5 (and=1) which leads to x=2 or x=3.
- By symmetry, for b=1, the only solution is y=5 which leads us to x=2 or x=3.
- For b=y=2, the only (repeated) solution is x=2
- Take b=2; y=3 we have two solutions x=1 or x=5.
- By symmetry, for b=3; y=2 we also have two solutions x=1 or x=5.
So basically we have 9 solutions : (x,y){ (1;2) ; (1;3) ; (2;1) ; (2;2) ; (2;5) ; (3;1) ; (3;5) ; (5;2) ; (5;3) }
This traduction

15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

