Bonne chance :++: :++:
Trois entiers strictement positifs
4 messages
- Page 1 sur 1
trois entiers strictement positifs
Bonjour : Existe-t-il trois entiers strictement positifs x,y, z vérifiant :
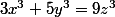
Bonne chance :++: :++:
Bonne chance :++: :++:
supposant que 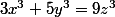 admet une solution (a,b,c)
admet une solution (a,b,c)
) => b est un multiple de 3(1)
=> b est un multiple de 3(1)
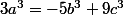 =>
=> 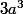 est un multiple de 9 (car b^3 et
est un multiple de 9 (car b^3 et 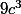 sont des mulitples de 9) => a est un multiple de 3(2)
sont des mulitples de 9) => a est un multiple de 3(2)
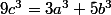 => 9c^3 est un multiple de
=> 9c^3 est un multiple de 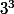 (car
(car 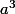 et
et 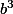 sont des multiple de
sont des multiple de 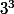 ) => c est un multiple de 3(3)
) => c est un multiple de 3(3)
(1),(2) et (3) me donne les droit de diviser a,b et c par 3
on a (a,b,c) une solution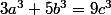
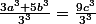
^3+5(b/3)^3=9(c/3)^3) (a/3,b/3,c/3) une solution (a/9,b/9,c/9) une solution (a/27,b/27,c/27) une solution ....((k-3) fois)...
(a/3,b/3,c/3) une solution (a/9,b/9,c/9) une solution (a/27,b/27,c/27) une solution ....((k-3) fois)... ) une solution quelque soit k de IN et en plus ces solution sont de IN ce qui est absurde
une solution quelque soit k de IN et en plus ces solution sont de IN ce qui est absurde
car il n'existe pas d'entiers strictement positifs qui rest encore entiers apres les divisé pas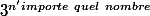
donc cette equation n'a pas de solution
(1),(2) et (3) me donne les droit de diviser a,b et c par 3
on a (a,b,c) une solution
car il n'existe pas d'entiers strictement positifs qui rest encore entiers apres les divisé pas
donc cette equation n'a pas de solution
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
