Nains de jardin
19 messages
- Page 1 sur 1
Nains de jardin
Sept nain sont assis autour d'une table ronde. Chacun a un verre devant lui. Il y'a du lait dans certains verres et il y'a au total 3L de lait. L'un des nains partage son lait uniformément entre les six autres sans en garder pour lui. En parcourant la table dans le sens inverse des aiguilles d'une montre, chaque autre nain fait de même. Après que le septième a partagé son lait, le contenu des verres est le même qu'au départ.
Trouver de quelle quantité de lait chaque nain disposait au départ.
Trouver de quelle quantité de lait chaque nain disposait au départ.
Zweig a écrit:(Où ça ? Je n'ai pas trouvé le topic)
ici peut-être:
http://forums.futura-sciences.com/thread207363.html
xD
:we:
Zweig a écrit:Oui je l'ai postée là-bas aussi, mais j'ai cru qu'il parlait de la section de ce forum.
xD au temps pour moi alors =)
pour ma part je l'ai lue récemment dans un livre mais j'ai oublié la réponse xD
çà se résouds comment çà ?? oO moi j'aurais dis comme lapras mais je ne vois pas comment faire plus rapide ^^
un indice ?? :p
Je n'ai rien compris donc si çà peut t'intéresser :
http://www.fimfa.ens.fr/exposes/2006/thouroude.pdf
lol ^^
http://www.fimfa.ens.fr/exposes/2006/thouroude.pdf
lol ^^
Bonsoir,
moi je n'ai pas regardé les divers liens proposés dans cette discussion, mais j'ai commencé à réfléchir au problème hier soir avant de me coucher pour en trouver la résolution ce matin en plein travail sur autre chose (lol).
Cela repose effectivement sur l'invariance par rotation du problème : le 2ème nain se retrouve exactement dans la même position que le 1er nain après que celui-ci ait réparti le contenu de son verre dans celui des 6 autres. En effet, puisqu'au bout d'un tour, lorsque le 7ème nain répartit également le contenu de son verre dans celui des autres, on revient à la situation initiale, alors si l'on continue, le second nain se retrouvera, une fois que le 1er nain aura réparti également le contenu de son verre dans celui des autres, dans la même situation qu'au tour d'avant. Cette situation étant exactement celle du 1er nain juste avant que celui-ci ne vide son verre.
Par ce raisonnement, il est donc établi que tout nain numéro n vérifie ce que le 1er nain vérifie, à savoir que "Le nain numéro n partage son lait uniformément entre les six autres sans en garder pour lui. En parcourant la table dans le sens inverse des aiguilles d'une montre, chaque autre nain fait de même. Après que le nain numéro n+6 [7] a partagé son lait, le contenu des verres est le même qu'au départ."
La situation tourne donc à chaque fois qu'un verre se vide : le verre qui le suit se trouve alors dans la situation dans laquelle celui qui le précèdait se trouvait juste avant lui, c'est-à-dire que les quantités dans chaque verre ont subit une rotation d'un verre. On le voit par exemple avec le verre vide, puisqu'il y en a toujours un, qui tourne à chaque fois.
Par conséquent, si l'on note le contenu initiale du verre numéro 1 , celui du verre numéro 2,
, celui du verre numéro 2,  , etc..., le contenu du verre numéro 2 après que le 1er nain a réparti le contenu de son verre doit être celui du verre numéro 1 avant qu'il ne répartisse le contenu de son verre (c'est-à-dire la quantité initiale x_1 de ce verre), or cette quantité vaut aussi
, etc..., le contenu du verre numéro 2 après que le 1er nain a réparti le contenu de son verre doit être celui du verre numéro 1 avant qu'il ne répartisse le contenu de son verre (c'est-à-dire la quantité initiale x_1 de ce verre), or cette quantité vaut aussi 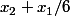 , donc :
, donc :
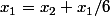
d'où
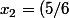 x_1)
De même,
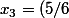 x_2 = (5/6)^{2} x_1) , etc...
, etc...
Du coup, on exprime la quantité initiale de chaque verre en fonction de celle de , puis comme on connaît la somme (3), on en déduit
, puis comme on connaît la somme (3), on en déduit  (somme des termes d'une suite géométrique) puis les autres quantités.
(somme des termes d'une suite géométrique) puis les autres quantités.
Vous êtes d'accord? :happy3:
moi je n'ai pas regardé les divers liens proposés dans cette discussion, mais j'ai commencé à réfléchir au problème hier soir avant de me coucher pour en trouver la résolution ce matin en plein travail sur autre chose (lol).
Cela repose effectivement sur l'invariance par rotation du problème : le 2ème nain se retrouve exactement dans la même position que le 1er nain après que celui-ci ait réparti le contenu de son verre dans celui des 6 autres. En effet, puisqu'au bout d'un tour, lorsque le 7ème nain répartit également le contenu de son verre dans celui des autres, on revient à la situation initiale, alors si l'on continue, le second nain se retrouvera, une fois que le 1er nain aura réparti également le contenu de son verre dans celui des autres, dans la même situation qu'au tour d'avant. Cette situation étant exactement celle du 1er nain juste avant que celui-ci ne vide son verre.
Par ce raisonnement, il est donc établi que tout nain numéro n vérifie ce que le 1er nain vérifie, à savoir que "Le nain numéro n partage son lait uniformément entre les six autres sans en garder pour lui. En parcourant la table dans le sens inverse des aiguilles d'une montre, chaque autre nain fait de même. Après que le nain numéro n+6 [7] a partagé son lait, le contenu des verres est le même qu'au départ."
La situation tourne donc à chaque fois qu'un verre se vide : le verre qui le suit se trouve alors dans la situation dans laquelle celui qui le précèdait se trouvait juste avant lui, c'est-à-dire que les quantités dans chaque verre ont subit une rotation d'un verre. On le voit par exemple avec le verre vide, puisqu'il y en a toujours un, qui tourne à chaque fois.
Par conséquent, si l'on note le contenu initiale du verre numéro 1
d'où
De même,
Du coup, on exprime la quantité initiale de chaque verre en fonction de celle de
Vous êtes d'accord? :happy3:
Une manière on ne peut plus sobre :
Dans l'ensemble des nains, chacun considéré au moment où il doit partager son lait, il y en a un qui dispose d'un maximum de lait. Appelons-le Max. Les six autres nains à sa droite disposent respectivement de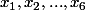 quantités de lait à partager. Max récupère de chacun
quantités de lait à partager. Max récupère de chacun 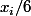 unités de lait. On a donc :
unités de lait. On a donc :
[CENTER]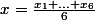 (1)[/CENTER]
(1)[/CENTER]
si on note le lait que le
le lait que le  -ème nain possède au moment où il doit partager. Or,
-ème nain possède au moment où il doit partager. Or, 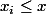 , pour tout i. Si cette inégalité était stricte, ne serait-ce qu'une fois, on ne pourrait pas avoir égalité au (1). Donc
, pour tout i. Si cette inégalité était stricte, ne serait-ce qu'une fois, on ne pourrait pas avoir égalité au (1). Donc 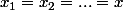 . Par conséquent, tous les nains partagent la même quantité de lait quand c'est leur tout de partager. On en déduit alors facilement que la distribution initiale de lait était 0, x/7, 2x/7, 3x/7, 4x/7, 5x/7, 6x/7. Comme la somme totale vaut 3, alors
. Par conséquent, tous les nains partagent la même quantité de lait quand c'est leur tout de partager. On en déduit alors facilement que la distribution initiale de lait était 0, x/7, 2x/7, 3x/7, 4x/7, 5x/7, 6x/7. Comme la somme totale vaut 3, alors 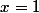 .
.
Dans l'ensemble des nains, chacun considéré au moment où il doit partager son lait, il y en a un qui dispose d'un maximum de lait. Appelons-le Max. Les six autres nains à sa droite disposent respectivement de
[CENTER]
si on note
Zweig a écrit:Par conséquent, tous les nains partagent la même quantité de lait quand c'est leur tout de partager. On en déduit alors facilement que la distribution initiale de lait était 0, x/7, 2x/7, 3x/7, 4x/7, 5x/7, 6x/7. Comme la somme totale vaut 3, alors.
Je suis tout à fait d'accord avec le raisonnement, mais par contre, je ne suis pas aussi d'accord avec le "on en déduit facilement" et surtout avec les quantités que tu annonces, quand je les compare à celles que je trouve. Car si 5x/7 est bien égal ) 5/6 * 6x/5, en revanche, 4x/7 n'est pas égal à (5/6) * 5x/7... Ma solution serait donc fausse?
En fait je me suis un peu emmêlé les pinceaux... Voici donc la nouvelle version de ma solution :
Comme tout verre n°i vérifie aussi bien l'énoncé que le verre n°1 juste avant de devoir se vider dans les autres verres (puisque, faisant un tour, on retombe sur la situation initiale), à chaque fois qu'un verre va se vider, il contient la même quantité que le verre n°1 en contenait avant qu'il ne se vide.
Ca c'est la partie raisonnement, qui me fait aboutir à la même conclusion que ton raisonnement. Ensuite vient ce qui correspond à ton "on en déduit facilement" :
En notant la quantité initiale dans le verre n°i, on a donc :
la quantité initiale dans le verre n°i, on a donc :
x (la quantité contenue dans le verre n°2 après que le 1 se soit vidé est égale à x_1 mais aussi au contenu initial
(la quantité contenue dans le verre n°2 après que le 1 se soit vidé est égale à x_1 mais aussi au contenu initial  du verre n°2 augmenté de
du verre n°2 augmenté de 
d'où
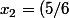 x_1)
De même,
)
donc
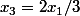
Il est clair que) , donc
, donc
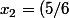 x_1)
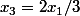

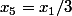
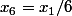
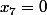
et=3)
donc
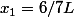
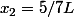
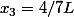
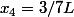
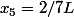
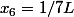
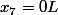
Et je retombe sur ta solution, Zweig. :happy3:
Comme tout verre n°i vérifie aussi bien l'énoncé que le verre n°1 juste avant de devoir se vider dans les autres verres (puisque, faisant un tour, on retombe sur la situation initiale), à chaque fois qu'un verre va se vider, il contient la même quantité que le verre n°1 en contenait avant qu'il ne se vide.
Ca c'est la partie raisonnement, qui me fait aboutir à la même conclusion que ton raisonnement. Ensuite vient ce qui correspond à ton "on en déduit facilement" :
En notant
x
d'où
De même,
donc
Il est clair que
et
donc
Et je retombe sur ta solution, Zweig. :happy3:
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
