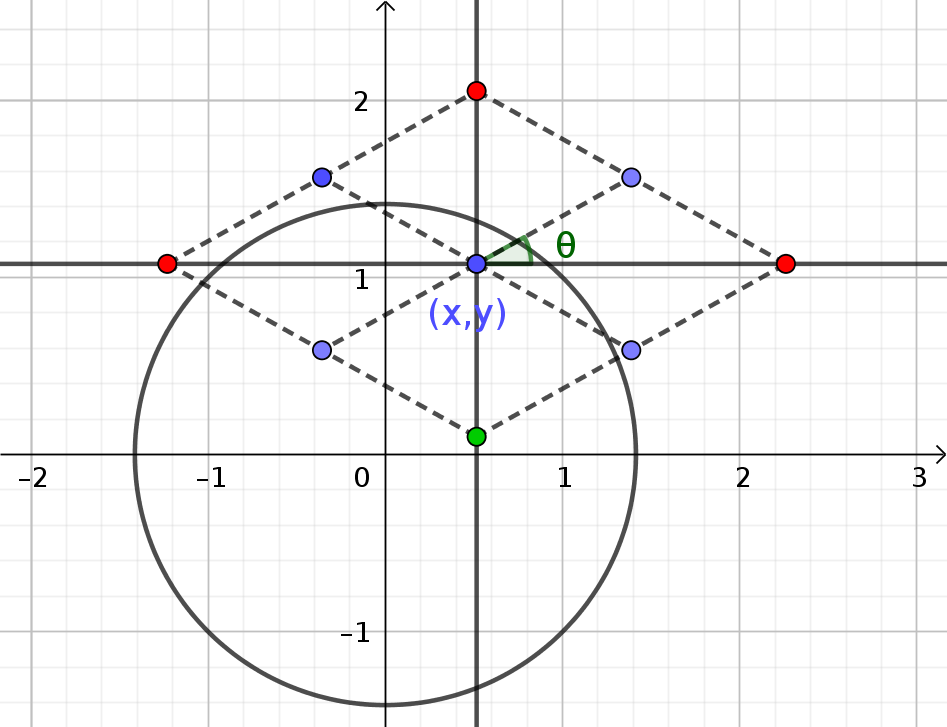
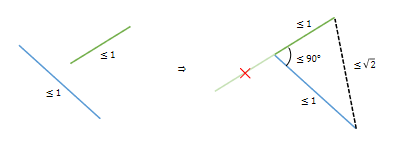
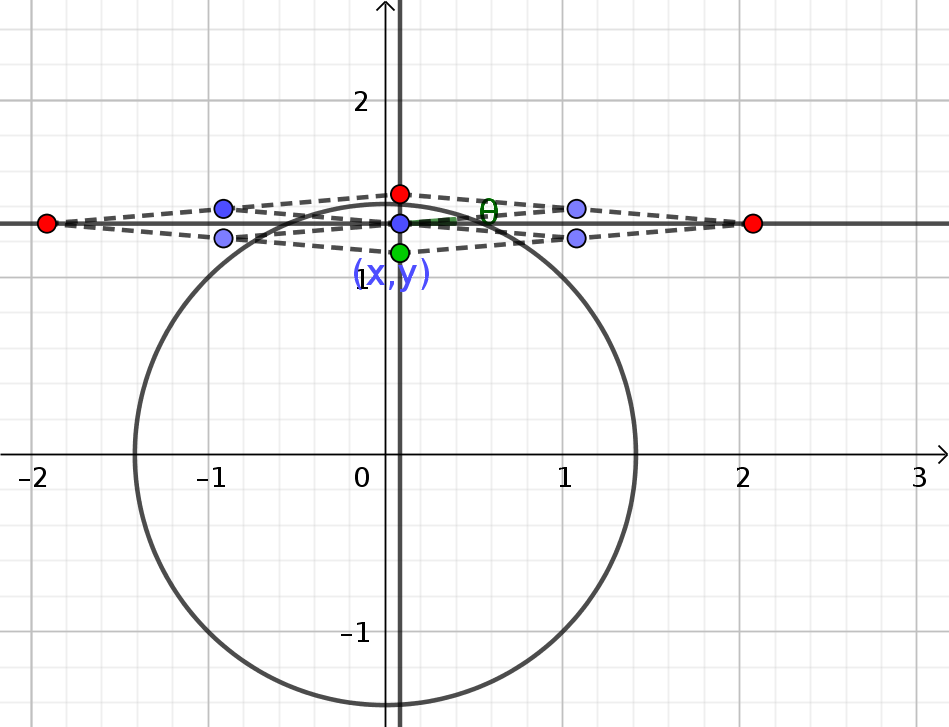
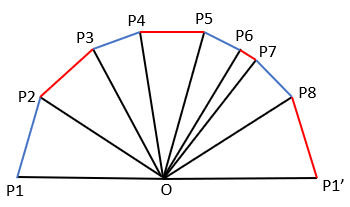
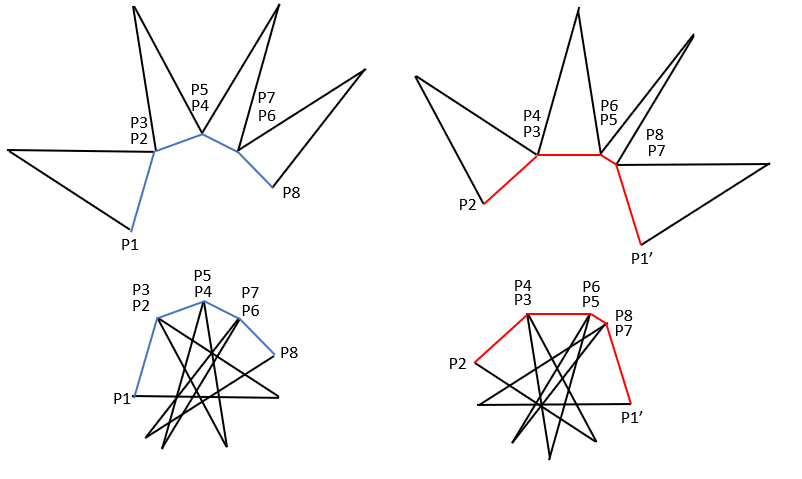
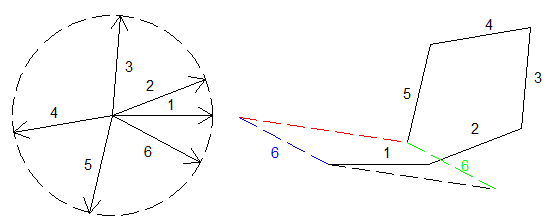
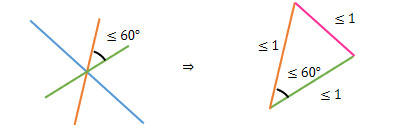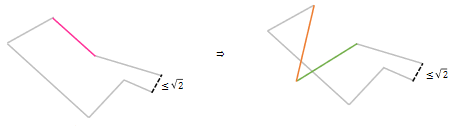On lance
On les translate (on ne peut donc pas changer leur direction) de sorte à les mettre bout à bout pour construire une chaine. L'objectif est d'avoir une distance entre les 2 extrémités de la chaine la plus petite possible. Essayons de donner le plus petit majorant de cette distance même si dans un premier temps n'importe quel majorant peut faire l'affaire.
Promis cette fois pas besoin d'outil informatique pour résoudre le problème même si ce n'est pas interdit pour avoir une idée, bon courage et bon amusement j'espère