Les nains et le bourreau
Olympiades mathématiques, énigmes et défis
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 04 Juil 2006, 13:03
par Patastronch » 04 Juil 2006, 13:03
Ogre : De quelle couleur est ton chapeau sâle nain ?
Nain : Noire
Nain de devant : Euh tu peux redire t as dis noireuuuh ou noir ?
Ogre : ...
Limite trop discret dans le cas contraire

De plus la parité est optimale innutile de chercher plus loin.
Par contre si jamais on a 3 couleurs de chapeau ... le modulo 3 ne marche pas aussi bien que la parité puisque je peut renseigner sur le nombre de chapeau que d'une seule couleur a la fois (probleme qu'on avaitpas avec 2 couleurs puisque rensigner sur une couleur rensiegne sur l'autre avec un petit complémentaire facil a faire). Donc il faudrait 2 sacrifiés au départ pour renseigner tout le monde sur toutes les couleurs (la troisieme couleur s'obtenant pas complémentarité également).
De maniere générale : N couleurs de chapeau = N-1 sacrifiés au départ avec la méthode similaire a la parité. Peut on faire mieu vous pensez ???
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 04 Juil 2006, 13:09
par nox » 04 Juil 2006, 13:09
BancH a écrit:Ogre : De quelle couleur est ton chapeau sâle nain ?
Nain : Blanche
Ogre : ...
Vraiment discrette comme stratégie.
hem...et pourtant ca ca serait correct grammaticalement ^^
de même que "quelle est ta nationalité? -> françaisE" même si tu es un homme
bon évidemment on suppose ici que pour que l'ogre ne soit pas choqué par une telle formule il doit avoir un minimum d'instruction ce qui n'est pas très conforme à l'image de l'ogre telle qu'on la connait :we:
Mais bon pour moi on a déjà quitté le domaine du féérique à partir du moment où l'ogre range ses victimes en file indienne avec des chapeaux de couleurs...
***********
Eh ba voila un superbe post bien inutile !
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 04 Juil 2006, 13:11
par Patastronch » 04 Juil 2006, 13:11
nox a écrit:hem...et pourtant ca ca serait correct grammaticalement ^^
de même que "quelle est ta nationalité? -> françaisE" même si tu es un homme
A ma connaissance chapeau est masculin.
[edit] ah ok, tu parles en fonction de la "couleur" et non du "chapeau" ok. De toute facon l'enononcé stipule qu'on ne peut dire que "blanc" ou "noir".
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 04 Juil 2006, 13:15
par BancH » 04 Juil 2006, 13:15
A mon avis les nains ont eu à peu près la même éducation et l'ogre soupsonnera sans doute quelque chose si la moitié des nains répond au masculin et l'autre moitié au féminin.
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 04 Juil 2006, 13:15
par nox » 04 Juil 2006, 13:15
Moui et de toute façon la vraie réponse a été donnée ^^
après c'est sur que comme le disais Jacques Lavau toutes les modulations et tonalités de la voix permettent d'envisager énormément d'autres stratégies moins subtiles.
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 04 Juil 2006, 13:19
par BancH » 04 Juil 2006, 13:19
Il est sous-entendu dans l'énoncé qu'il n'y a pas de variante orale possible, comme il est sous-entendu que les nains ne peuvent pas regarder eux-même leur chapeau ou discuter entre eux.
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 04 Juil 2006, 13:20
par Sdec25 » 04 Juil 2006, 13:20
En ayant un type de réponse binaire, en ne donnant qu'un seule information (noir ou blanc) la bonne réponse est celle avec les nombres pairs et impairs.
Après il reste toujours la télépathie :ptdr:
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 04 Juil 2006, 14:24
par Patastronch » 04 Juil 2006, 14:24
Moi je dis 100 nains sur un bourreau ca se tente...
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 04 Juil 2006, 15:09
par nox » 04 Juil 2006, 15:09
y en a peut etre pas 100
et a 2 sur un ogre c'est tendu...meme si c'est teigneux un nain
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 04 Juil 2006, 15:14
par BancH » 04 Juil 2006, 15:14
Patastronch a écrit:De maniere générale : N couleurs de chapeau = N-1 sacrifiés au départ avec la méthode similaire a la parité. Peut on faire mieu vous pensez ???
Pour
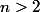
, le nombre maximum de morts avec une stratégie optimale est bien

seulement si
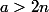
avec

le nombre de nains total.
Mais cette stratégie ne fonctionne que si les nains connaissent les couleurs des chapeaux des nains déjà interrogés.
Et comme ce n'est pas le cas, la meilleure tactique est qu'un nain sur deux dit la couleur du chapeau du nain juste devant lui, ce qui permet au maximum
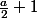
morts.
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 04 Juil 2006, 15:20
par nox » 04 Juil 2006, 15:20
BancH a écrit:Pour
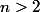
, le nombre maximum de morts avec une stratégie optimale est bien

seulement si
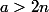
avec

le nombre de nains total.
et ca serait quoi cette stratégie?
Avec 3 couleurs de chapeaux il faut sacrifier les 2 premiers nains en utilisant la parité donc on peut faire mieux que n-1 morts non?
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 04 Juil 2006, 15:25
par nox » 04 Juil 2006, 15:25
j ai supprimé ^^
j'ai dit nimp :)
L'information du premier nain est evidemment perdue si le 2eme nain répond faux dans un cas avec plus de 2 couleurs
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 04 Juil 2006, 15:33
par BancH » 04 Juil 2006, 15:33
Exemple:
Trois couleurs, donc deux sacrifices.
=> noir noir blanc rose rose rose blanc
=>Le premier indique la parité du nombre de chapeaux noirs devant lui :
impairLe second celle du nombre de chapeaux blancs devant lui :
pairLe troisième doit connaître ou calculer le nombre de nains total et déduire la parité du nombre de chapeaux roses :
pair Il a donc trois choix : noir, blanc ou rose ...
Cette stratégie ne fonctionne que si les  premiers nains à être interrogés on tous des chapeaux différents.
premiers nains à être interrogés on tous des chapeaux différents.
Edit : Il a supprimé son message - -
-
ayoub879
- Messages: 1
- Enregistré le: 31 Jan 2020, 18:19
-
 par ayoub879 » 31 Jan 2020, 18:30
par ayoub879 » 31 Jan 2020, 18:30
Comme chaque nain connait le chapeau de celui qui est devant lui, le 1er qui passe enlève son chapeau et le pose * et se place en dernier du fil, et prend le chapeau de celui d'avant et vise versa, le 1er du fil se trouve sans chapeau se replace en dernier et reprend celui du premier*.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 31 Jan 2020, 19:25
par Sa Majesté » 31 Jan 2020, 19:25
Félicitations, tu viens de battre le record du monde de déterrage : 13 ans 6 mois et 27 jours

-
mathelot
 par mathelot » 31 Jan 2020, 21:10
par mathelot » 31 Jan 2020, 21:10
bonsoir,
le 1er nain interrogé doit indiquer, à haute voix et entendu de tous les nains, la parité des chapeaux noirs et des chapeaux blancs. Il risque d'être tué car il répond de manière codifiée et conventionnelle.
Après lui, l'avant dernier nain connait la couleur de son chapeau, il est de même couleur que la parité erronée
qu'il constate. Et ainsi de suite..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
