Kasstet la famille nombre
Olympiades mathématiques, énigmes et défis

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 26 Avr 2009, 17:09
par leon1789 » 26 Avr 2009, 17:09
Imod a écrit:Une petite idée : supposer qu'il y a deux élément de la même génération portant le même nom et remonter pour trouver la contradiction ( c'est très court ) .
Imod
Avec les indications que tu donnes (ancêtres de n²-1), je comprends ton argument. J'ai alors l'impression que ta petite idée un "raisonnement par l'absurde utilisant un élément n² avec n minimum tel que...", c'est bien ça ?
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 26 Avr 2009, 17:38
par Imod » 26 Avr 2009, 17:38
Par l'absurde :doh: , je ne me le permettrai pas :zen:
En fait il n'y a même pas besoin de supposer que

minimal , il suffit de remonter en parallèles les ancêtres de
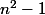
et

pour se rendre compte qu'il y a problème ( ne pas oublier qu'un ancêtre a un nom "inférieur" à celui de son fils ) .
Imod

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 26 Avr 2009, 17:46
par leon1789 » 26 Avr 2009, 17:46
Imod a écrit:Par l'absurde :doh: , je ne me le permettrai pas :zen:
aaah tu as peurrrrrrrrr d'avouer !!! :ptdr:
Imod a écrit:En fait il n'y a même pas besoin de supposer que

minimal , il suffit de remonter en parallèles les ancêtres de
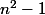
et

pour se rendre compte qu'il y a problème (ne pas oublier qu'un ancêtre a un nom "inférieur" à celui de son fils ) .
Imod
oui, il y a d'un coté 2n-1 ancêtres minimum, alors que de l'autre n maximum... un truc comme ça :we:
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 26 Avr 2009, 17:54
par Imod » 26 Avr 2009, 17:54
Tout à fait :++:
Imod
-
C.A.L
- Messages: 9
- Enregistré le: 17 Avr 2009, 15:51
-
 par C.A.L » 28 Avr 2009, 13:17
par C.A.L » 28 Avr 2009, 13:17
EUH...vous pourriez m'expliker ?car je ne comprend rien et c'est pour demain :marteau: ...merci
-
C.A.L
- Messages: 9
- Enregistré le: 17 Avr 2009, 15:51
-
 par C.A.L » 28 Avr 2009, 15:25
par C.A.L » 28 Avr 2009, 15:25
j'ai remonté come vs me lavié di lé ancètre de n et n²-1 é jpens ke sa done sa :
racine de n n-1 racine de (n²-1) n²-2
\ / \ /
n n²-1
\ /
n²
et avec sa c sur kje pe dir ke 2 nombre de la mem génération nauron jamai le mem nom. Ske sété sa ke tu voulé dir lorke tu parlé d' un raisonemen par l'absurde?
-
C.A.L
- Messages: 9
- Enregistré le: 17 Avr 2009, 15:51
-
 par C.A.L » 28 Avr 2009, 15:47
par C.A.L » 28 Avr 2009, 15:47
je pense avoir compris ce que vous m'avez dit et si on remonte les ancètres de n² je pense que sa donne:
racine de n.....n-1.......racine de (n²-1).....n²-2
............\......./..........................\.............../
...............n...................................n²-1
.................\................................./
.................................n²
avec sa je peux donc dire qu'il existe pas 2 membres d'une meme génération avec le meme nom. es ce que c 'est sa que vous voulé parlé kan vous me parlé de raisonement par l' absurde?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 28 Avr 2009, 16:40
par Timothé Lefebvre » 28 Avr 2009, 16:40
Je te rappelle que nous ne sommes pas sur MSN ici !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
