IMO "shortlist"

par **Zweig** » 17 Jan 2009, 17:26

Salut,

J'aimerais savoir si quelqu'un a une solution qui n'utilise que de la géométrie "classique", i.e, sans les complexes ? J'ai trouvé une solution utilisant les complexes et je peine pour trouver une solution géométrique "classique" :

Soit ABCD un quadrilatère convexe vérifiant

. Quatre triangles équilatéraux sont construits sur les côtés du quadrilatère, à l'extérieur de celui-ci. Soient

,

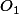
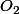
et

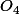
respectivement les centres des triangles construits sur les côtés AB, BC, CD et AD.

Montrer que

et

sont perpendiculaires.

par **Zweig** » 17 Jan 2009, 19:13

Tout compte fait, j'ai trouvé une solution n'utilisant pas les nombres complexes :we: ... Je suis quand même intéressé pour voir les vôtres !

par **yos** » 17 Jan 2009, 20:15

C'est assez facile de montrer que le parallélogramme UVWX des milieux de ABCD est ici un losange (

).

par **Zweig** » 17 Jan 2009, 23:11

Sauf que je ne vois pas en quoi ça permet de conclure :marteau:

par **Imod** » 22 Jan 2009, 00:21

yos a écrit:C'est assez facile de montrer que le parallélogramme UVWX des milieux de ABCD est ici un losange ().

Oui , mais le travail est loin d'être fini :zen:

Imod

par **yos** » 23 Jan 2009, 12:40

Imod a écrit:Oui , mais le travail est loin d'être fini

Après je montre que

en quelques lignes de produit scalaire. C'est pas super joli car j'ai pas essayé de nettoyer ce que j'avais en premier jet, mais ça marche.

par **yos** » 27 Jan 2009, 19:14

L'exercice c'est

.
Je propose la variante :

.

IMO "shortlist"

IMO "shortlist"

Qui est en ligne