IMO 1988

[LjjMaths]

Salut à tous,
J'ai trouvé un exo qui a l air sympathique mais je bloque complètement :
Soit des entiers positifs tq
Il faut prouver que est le carré d un entier

Merci d avance

[Ben314]

Salut,
C'est un archi archi archi classique (et à mon avis parce qu'il y a pas mal de monde... dont moi... qui trouve la preuve super marrante).
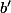
L'idée, c'est d'écrire sous la forme et d'introduire la deuxième racine de l'équation de façon à trouver une autre solution "plus petite" (mais avec le même ).

Avec ça comme indic., tu devrait y arriver (mais y'a des petites astuces sur les inégalités à démontrer. . .)

[LjjMaths]

D'accord merci bcp Ben, merci de ne pas m avoir donné la reponse directement c'est sympa, comme ca je peux chercher