Équiproblème

[Lostounet]

Je ne pense pas. La formule connue est plutôt



pour x, y et z des réels quelconques (par forcément les angles d'un triangle) et cette dernière ne m'a pas l'air équivalente avec la tienne ...

Yo, la formule ne vient pas de moi mais de:

http://www.wolframalpha.com/input/?i=cos%28x+%2B+y+%2B+z%29

Elle est fausse? :hum:


Je vous remercie de vos réponses, je vais essayer de les comprendre

[Zweig]

Non elle est juste ... J'avais pas pensé à développer comme ça :lol3:

[Lostounet]

Excuse-moi Dlzlogic, mais je ne comprends pas ta méthode :/
Pourrais-tu me l'expliquer autrement?

[Dlzlogic]

Excuse-moi Dlzlogic, mais je ne comprends pas ta méthode :/
Pourrais-tu me l'expliquer autrement?

Le principe de la méthode est général : on construit un triangle semblable au triangle cherché et à l'aide d'une relation on le construit à la dimension réelle. Si on peut le construire, on peut le calculer.
Pour y arriver, je suis parti du triangle équilatéral, et j'ai dessiné les symétriques de M par rapport aux côtés. En fait pour être franc, ce sont les dimensions 3,4,5 qui m'ont mis sur la voie, mais c'est vrai aussi pour n'importe quelles dimensions (tant qu'elles peuvent être les côtés d'un triangle).
En fait, je n'utilise pas le fait que le triangle est rectangle.
Je pense que si tu suis le même cheminement ça va s'éclairer. Un autre exemple typique d'utilisation de cette méthode est de construire un triangle connaissant la longueur des 3 hauteurs (de mémoire).
Mais il est vrai que ce n'est pas très facile à voir.

[Doraki]

comme j'ai horreur de faire des calculs moins symétriques que le résultat, je recommence :

Comme ils sont dans le plan, les 3 vecteurs AM, BM, CM sont liés, donc

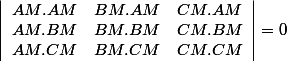
(mon calcul précédent revenait à faire pareil mais avec la famille AM,AB,AC)

On exprime chaque entrée en fonction de a,b,c,x et on multiplie tout par 2 :



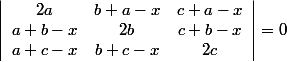
Si x=0, on voit la liaison *évidente* (c-b)*C1 + (a-c)*C2 + (b-a)*C3 = 0, donc le déterminant est nul lorsque x=0.
Donc ce déterminant est un polynôme de degré 3 qui est multiple de x.

Donc on développe le déterminant dans la joie (ou alors on se contente de calculer les coefficients devant x^3, xab, xa², et x²a), on divise par x, et on obtient normalement l'équation homogène de degré 2 a²+b²+c²+x² = ab+ac+ax+bc+bx+cx.

Bon ça n'explique pas pourquoi x est interchangeable avec les autres trucs.
Aussi mon déterminant a le défaut d'être multiple de x, donc le déterminant qui lui est invariant par tout serait un truc du genre

| M 0 |
| 0 1/x |
ce qui est tout de même affreusement moche.

J'aimerais bien faire rentrer un 4ème vecteur, par exemple AB, dans ma famille de vecteurs pour avoir une matrice 4*4 qui ait une chance d'être symétrique, mais faudrait aussi rajouter une 3ème dimension au problème, je vois pas trop à quoi ça pourrait correspondre.

[Dlzlogic]

Je me demande si ce type de problème ne se résout pas avec une inversion. Mais là j'ai oublié comment ça marche.

[Jota Be]

Je n'arrive plus à suivre depuis un moment, vous savez :ptdr:
Bon, bonne nuit à tous, je vais peut-être y réfléchir demain.

:livre: puis :dodo: !

[Nightmare]

Dans l'idée du déterminant de Doraki, on peut aussi dire qu'on à affaire à un tétraèdre de volume nul.

[Lostounet]

Je viens de trouver une solution !!! :D
Et j'ai trouvé la même chose que Doraki, je vais essayer de la poster dans quelques instants :)

[Imod]

J'avais cherché ce problème il y a un un an ou deux , et j'étais arrivé à cet hexagone qui donne la solution dans le cas général à peu de frais .



Il suffit d'exprimer son aire de deux façons .

Imod

PS : pour le cas 3,4,5 il y a une solution type "quickie" car ce sont les côtés d'un triangle rectangle .

[Doraki]

En fait c'est normal qu'on obtienne une condition symétriques en les 4 distances.

Après, moi je suis pas tellement au courant des tétraèdres de Nightmare :/

[Lostounet]

Je me suis inspiré du post de DlzLogic pour effectuer les tracés suivants:





J'ai construit des symétriques de M par rapport aux côtés, et j'ai ainsi obtenu des cerfs-volants comme le montre la figure.

On sait que (ou Wikipedia m'a fait savoir que...) l'aire d'un cerf-volant est donnée par la formule:



Avec la mesure de l'angle formé par les côtés inégaux a et b.

Les côtés devenant axes de symétrie, l'aire du triangle est la somme des aires des cerfs-volants divisée par 2.

On peut écrire:


Soit bien entendu:


Ensuite, nous avons déjà une idée des cosinus des angles x, y et z (par Al-kashi dans les petits triangles).

Nous écrivons chacun des sinus en fonction des cos des angles qui correspondent,
par exemple:


Avec

Nous obtenons après de longs périples, l'équation suivante:



Dont l'unique solution à retenir est: (par Wolfram)
(je ne sais pas pourquoi j'ai pas trouvé l'autre soluce de Doraki...).

Un peu bourrin, je sais, mais au moins j'ai pu apprendre pas mal de chose grâce à cet exercice