Énigme je n'y arrive pas :(

[St3pff]

Bonjour,
Pourriez vous m'aider sur cette énigme que je n'arrive pas à résoudre. Merci de bien décomposer que je puisse comprendre svp. Merci d'avance.

C'est un homme sur son vélo qui roule sur un pont à sens unique, mais qui n'a pas la place pour qu'une voiture puisse le dépasser. On averti le cycliste qu'une voiture qui n'a pas plus de freins et arrive derrière lui à 120 km, on sait que le cycliste qui a déjà parcouru 7/20ème du pont peut soit faire demi tour ou soit continuer jusqu'à la fin du pont pour éviter la voiture. A quelle vitesse est le cycliste ?

Au secours il me manque les bases des mathématiques. J'ai réellement besoin de comprend.

[GaBuZoMeu]

Bonjour,

comme d'habitude quand un problème mathématique est trop "habillé" on oublie de dire des hypothèses et le problème ne fait plus sens. Il y a aussi des coquilles dans la transcription : il s'agit sans doute de 120 km/h pour la vitesse de la voiture ?
Si la voiture qui arrive est à 60km du pont, le cycliste aura sûrement tout son temps pour dégager le pont bien avant que l'automobiliste arrive.

Ce qui n'est pas dit c'est sans doute que
- si le cycliste poursuit sa route, il arrive à la fin du pont exactement quand l'automobiliste y arrive,
- si le cycliste fait demi-tour pour regagner le début du pont, il y arrive.
exactement quand l'automobiliste arrive au début du pont.

On peut alors résoudre le problème.
On note la longueur du pont,
la vitesse du cycliste,
la vitesse de l'automobiliste (on la connaît),
le temps que met le cycliste à rejoindre le début du pont s'il fait demi-tour,
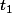le temps que met le cycliste à atteindre la fin du pont s'il poursuit sa route.

On écrit les équations qui relient tout ça en utilisant les hypothèses, surtout celles que j'ai ajoutées. On essaie d'en tirer (et on y arrive).

[St3pff]

Merci énormément. Peux tu me montrer l'équation nécessaire à effectuer stp ? Je voudrais le résultat.
Cordialement

[GaBuZoMeu]

Et moi, je voudrais que tu y mettes un peu du tien.
Pour commencer, peux tu exprimer la relation qui lie la longueur du pont , la vitesse du cycliste , et le temps qu'il met à revenir au début du pont ? Ça me semble assez élémentaire, n'est-ce-pas, de trouver une relation entre la vitesse, la distance à parcourir et le temps mis à la parcourir ?

[St3pff]

Ok merci.

[GaBuZoMeu]

Alors, quelle est cette relation ?

[St3pff]

J'ai arrêté l'école très tôt, si je demande de l'aide et la solution c'est pas pour jubiler en disant j'ai la solution car personne ne sait que j'essaye d'apprendre les mathématiques . C'est juste que maintenant que j'ai vieilli je voudrais apprendre les maths et d'habitude on m'explique et après je décortique tout pour comprendre et je vais apprendre les bases via des tutoriels. Si sa parle de fraction j'apprends les fractions si c'est les % je vais apprendre enfin il me semble que tu sois suffisamment intelligent pour comprendre ce que je recherche. Mais te prend pas la tête je vais aller ailleur. Bonne journée. Je te souhaite le meilleur dans la vie.

[GaBuZoMeu]

Il me semblait que la relation :
durée du parcours x vitesse = distance parcourue
faisait partie des compétences de la vie courante.