Son cube possède
Diviseurs positifs
3 messages
- Page 1 sur 1
Diviseurs positifs
Un nombre du bonheur est un nombre entier strictement positif.
Son cube possède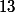 fois plus de diviseurs positifs que lui. Combien de diviseurs positifs un nombre du bonheur possede-t-il?
fois plus de diviseurs positifs que lui. Combien de diviseurs positifs un nombre du bonheur possede-t-il?
Son cube possède
Re: Diviseurs positifs
Salut,
Si la décomposition en facteurs premier (distincts) de est
est 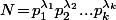 (avec
(avec 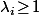 ) alors il est clair que les diviseurs positifs de N sont très précisément les nombres de la forme
) alors il est clair que les diviseurs positifs de N sont très précisément les nombres de la forme 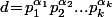 avec
avec  et il y en a donc
et il y en a donc \!=\!(\lambda_1\!+\!1)(\lambda_2\!+\!1)...(\lambda_k\!+\!1)) (= nombre de possibilités pour les
(= nombre de possibilités pour les 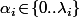 ).
).
Vu que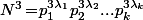 l'énoncé est donc équivalent à l'équation :
l'énoncé est donc équivalent à l'équation :
(3\lambda_2\!+\!1)...(3\lambda_k\!+\!1)\!=\!13(\lambda_1\!+\!1)(\lambda_2\!+\!1)...(\lambda_k\!+\!1))
Comme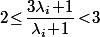 on a
on a 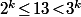 ce qui montre que
ce qui montre que 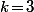 .
.
Comme 13 est premier on a (par exemple)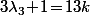 avec
avec 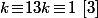 donc
donc 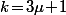 et
et 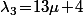 avec
avec 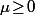 .
.
On a donc(3\lambda_2\!+\!1)(3\mu\!+\!1)\!=\!(\lambda_1\!+\!1)(\lambda_2\!+\!1)(13\mu\!+\!5)) qui peut s'écrire sous la forme
qui peut s'écrire sous la forme
(7\lambda_2\!-\!2)\!-\!39\Big)\mu+\Big((2\lambda_1\!-\!1)(2\lambda_2\!-\!1)\!-\!5\Big)=0)
Or,(7\lambda_2\!-\!2)\!>\!39) sauf pour (1,1) et
sauf pour (1,1) et (2\lambda_2\!-\!1)\!>\!5) sauf pour (1,1) ; (1,2) et (1,3).
sauf pour (1,1) ; (1,2) et (1,3).
L'étude des seuls cas restant conduit à une unique solution :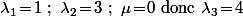 :
:
N admet (1+1)(3+1)(4+1) = 40 diviseurs.
N^3 admet (3x1+1)(3x3+1)(3x4+1) = 40 x 13 diviseurs.
(et le plus petit nombre du bonheur est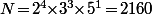 )
)
Si la décomposition en facteurs premier (distincts) de
Vu que
Comme
Comme 13 est premier on a (par exemple)
On a donc
Or,
L'étude des seuls cas restant conduit à une unique solution :
N admet (1+1)(3+1)(4+1) = 40 diviseurs.
N^3 admet (3x1+1)(3x3+1)(3x4+1) = 40 x 13 diviseurs.
(et le plus petit nombre du bonheur est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
